
【題目】若對任意實數![]() 都有函數
都有函數![]() 的圖象與直線
的圖象與直線![]() 相切,則稱函數
相切,則稱函數![]() 為“恒切函數”,設函數
為“恒切函數”,設函數![]() ,其中
,其中![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)已知函數![]() 為“恒切函數”,
為“恒切函數”,
①求實數![]() 的取值范圍;
的取值范圍;
②當![]() 取最大值時,若函數
取最大值時,若函數![]() 也為“恒切函數”,求證:
也為“恒切函數”,求證:![]() .
.
【答案】(1)見解析;(2)![]()
【解析】分析:(1)求出![]() ,分兩種情況討論
,分兩種情況討論![]() 的范圍,在定義域內,分別令
的范圍,在定義域內,分別令![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 增區間,
增區間,![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 的減區間;(2)①設切點為
的減區間;(2)①設切點為![]() ,求出
,求出![]() ,設
,設![]() ,根據函數的單調性求出
,根據函數的單調性求出![]() 故實數
故實數![]() 的取值范圍為
的取值范圍為![]() ;②當
;②當![]() 取最大值時,
取最大值時,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,因為函數
,因為函數![]() 也為“恒切函數”,故存在
也為“恒切函數”,故存在![]() ,使得
,使得![]() ,
,![]() ,由
,由![]() 得
得![]() ,
,![]() ,設
,設![]() ,,根據函數的單調性證明即可.
,,根據函數的單調性證明即可.
詳解:(1)![]() .當
.當![]() 時,
時,![]() 恒成立,函數
恒成立,函數![]() 在
在![]() 上單調遞減;
上單調遞減;
當![]() 時,
時,![]() 得
得![]() ,由
,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
得函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上遞增.
上遞增.
(2)①若函數![]() 為“恒切函數”,則函數
為“恒切函數”,則函數![]() 的圖象與直線
的圖象與直線![]() 相切,
相切,
設切點為![]() ,則
,則![]() 且
且![]() ,即
,即![]() ,
,![]() .
.
因為函數![]() 為“恒切函數”,所以存在
為“恒切函數”,所以存在![]() ,使得
,使得![]() ,
,![]() ,即
,即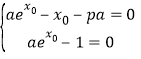 ,得
,得![]() ,
,![]() ,設
,設![]() .
.
則![]() ,
,![]() ,得
,得![]() ,
,![]() 得
得![]() ,
,
故![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,從而
上單調遞減,從而![]()
故實數![]() 的取值范圍為
的取值范圍為![]() .
.
②當![]() 取最大值時,
取最大值時,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,因為函數
,因為函數![]() 也為“恒切函數”,故存在
也為“恒切函數”,故存在![]() ,使得
,使得![]() ,
,![]() ,由
,由![]() 得
得![]() ,
,![]() ,設
,設![]() ,
,
則![]() ,
,![]() 得
得![]() ,
,![]() 得
得![]() ,
,
故![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
1.在單調遞增區間![]() 上,
上,![]() ,故
,故![]() ,由
,由![]() ,得
,得![]() ;
;
2. 在單調遞增區間![]() 上,
上,![]() ,
,
![]() ,又
,又![]() 的圖象在
的圖象在![]() 上不間斷,
上不間斷,
故在區間![]() 上存在唯一的
上存在唯一的![]() ,使得
,使得![]() ,故
,故![]() .
.
此時由![]() ,得
,得![]() ,
,
函數![]() 在
在![]() 上遞增,
上遞增,![]() ,
,![]() ,故
,故![]() .
.
綜上所述,![]() .
.


科目:高中數學 來源: 題型:
【題目】2018年高考成績揭曉,某高中再創輝煌,考后學校對于單科成績逐個進行分析:現對甲、乙兩個文科班的數學成績進行分析,規定:大于等于135分為優秀,135分以下為非優秀,成績統計后,得到如下的![]() 列聯表,且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為
列聯表,且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為![]() .
.
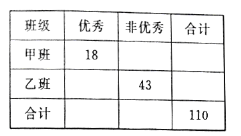
(1)請完成上面的列聯表;
(2)請問:是否有75%的把握認為“數學成績與所在的班級有關系”?
(3)用分層抽樣的方法從甲、乙兩個文科班的數學成績優秀的學生中抽取5名學生進行調研,然后再從這5名學生中隨機抽取2名學生進行談話,求抽到的2名學生中至少有1名乙班學生的概率.
參考公式:![]() (其中
(其中![]() )
)
參考數據:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2016·重慶高二檢測)如圖,三棱柱ABC-A1B1C1中,側棱垂直底面,∠ACB=90°,AC=BC=![]() AA1,D是棱AA1的中點.
AA1,D是棱AA1的中點.

(1)證明:平面BDC1⊥平面BDC.
(2)平面BDC1分此棱柱為兩部分,求這兩部分體積的比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大型綜藝節目《最強大腦》中,有一個游戲叫做盲擰魔方,就是玩家先觀察魔方狀態并進行記憶,記住后蒙住眼睛快速還原魔方,盲擰在外人看來很神奇,其實原理是十分簡單的,要學會盲擰也是很容易的.根據調查顯示,是否喜歡盲擰魔方與性別有關.為了驗證這個結論,某興趣小組隨機抽取了50名魔方愛好者進行調查,得到的情況如下表所示:
喜歡盲擰 | 不喜歡盲擰 | 總計 | |
男 | 22 | ▲ | 30 |
女 | ▲ | 12 | ▲ |
總計 | ▲ | ▲ | 50 |
表1
并邀請這30名男生參加盲擰三階魔方比賽,其完成情況如下表所示:
成功完成時間(分鐘) | [0,10) | [10,20) | [20,30) | [30,40] |
人數 | 10 | 10 | 5 | 5 |
表2
(1)將表1補充完整,并判斷能否在犯錯誤的概率不超過0.025的前提下認為是否喜歡盲擰與性別有關?
(2)根據表2中的數據,求這30名男生成功完成盲擰的平均時間(同一組中的數據用該組區間的中點值代替);
(3)現從表2中成功完成時間在[0,10)內的10名男生中任意抽取3人對他們的盲擰情況進行視頻記錄,記成功完成時間在[0,10)內的甲、乙、丙3人中被抽到的人數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
附參考公式及數據:,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是直角梯形,側棱
是直角梯形,側棱![]() 底面
底面![]() ,
, ![]() 垂直于
垂直于![]() 和
和![]() ,
,![]() 為棱
為棱![]() 上的點,
上的點,![]() ,
,![]() .
.

(1)若![]() 為棱
為棱![]() 的中點,求證:
的中點,求證:![]() //平面
//平面![]() ;
;
(2)當![]() 時,求平面
時,求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值;
所成的銳二面角的余弦值;
(3)在第(2)問條件下,設點![]() 是線段
是線段![]() 上的動點,
上的動點,![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求當
,求當![]() 取最大值時點
取最大值時點![]() 的位置.
的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市舉行“中學生詩詞大賽”,分初賽和復賽兩個階段進行,規定:初賽成績大于90分的具有復賽資格,某校有800名學生參加了初賽,所有學生的成績均在區間(30,150]內,其頻率分布直方圖如圖.則獲得復賽資格的人數為()

A.640B.520C.280D.240
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com