
【題目】已知函數![]()
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)若方程![]() 在區間(0,+)上有實數解,求實數a的取值范圍;
在區間(0,+)上有實數解,求實數a的取值范圍;
(3)若存在實數![]() ,且
,且![]() ,使得
,使得![]() ,求證:
,求證:![]() .
.
【答案】(1)函數![]() 的單調減區間為
的單調減區間為![]() 和
和![]() ,單調增區間為
,單調增區間為![]() .(2)
.(2)![]() (3)見解析
(3)見解析
【解析】
試題分析:(1)![]() 時,
時,![]() ,分段求出導函數,分別令
,分段求出導函數,分別令![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 增區間,
增區間,![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 的減區間;(2)設
的減區間;(2)設![]() ,則
,則![]() ,所以
,所以![]() 在區間
在區間![]() 上有解,等價于
上有解,等價于![]() 在區間
在區間![]() 上有解,設
上有解,設![]() ,對利用導數研究函數
,對利用導數研究函數![]() 的單調性,結合函數圖象及零點存在定理,即可得到符合題意的
的單調性,結合函數圖象及零點存在定理,即可得到符合題意的![]() 的取值范圍即可;(3)先排除
的取值范圍即可;(3)先排除![]() 的情況,到
的情況,到![]() ,利用導數研究函數的單調性,分別求出最大值與最小值,問題轉化為
,利用導數研究函數的單調性,分別求出最大值與最小值,問題轉化為![]() 解得
解得![]() ,所以
,所以![]() .
.
試題解析:(1)當![]() 時,
時,![]()
當![]() 時,
時,![]() ,則
,則![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() (舍),所以
(舍),所以![]() 時,
時,![]() ,
,
所以函數![]() 在區間
在區間![]() 上為減函數.
上為減函數.
當![]() 時,
時,![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() ,當
,當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
所以函數![]() 在區間
在區間![]() 上為減函數,在區間
上為減函數,在區間![]() 上為增函數,
上為增函數,
且![]() .
.
綜上,函數![]() 的單調減區間為
的單調減區間為![]() 和
和![]() ,單調增區間為
,單調增區間為![]() .
.
(2)設![]() ,則
,則![]() ,所以
,所以![]() ,
,
由題意,![]() 在區間
在區間![]() 上有解,
上有解,
等價于![]() 在區間
在區間![]() 上有解.
上有解.
記![]() ,
,
則![]() ,
,
令![]() ,因為
,因為![]() ,所以
,所以![]() ,故解得
,故解得![]() ,
,
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
所以函數![]() 在區間
在區間![]() 上單調遞減,在區間
上單調遞減,在區間![]() 上單調遞增,
上單調遞增,
故函數![]() 在
在![]() 處取得最小值
處取得最小值![]() .
.
要使方程![]() 在區間
在區間![]() 上有解,當且僅當
上有解,當且僅當![]() ,
,
綜上,滿足題意的實數a的取值范圍為![]() .
.
(3)由題意,![]() ,
,
當![]() 時,
時,![]() ,此時函數
,此時函數![]() 在
在![]() 上單調遞增,
上單調遞增,
由![]() ,可得
,可得![]() ,與條件
,與條件![]() 矛盾,所以
矛盾,所以![]() .
.
令![]() ,解得
,解得![]() ,
,
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
所以函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
若存在![]() ,
,![]() ,則
,則![]() 介于m,n之間,
介于m,n之間,
不妨設![]() ,
,
因為![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,且
上單調遞增,且![]() ,
,
所以當![]() 時,
時,![]() ,
,
由![]() ,
,![]() ,可得
,可得![]() ,故
,故![]() ,
,
又![]() 在
在![]() 上單調遞減,且
上單調遞減,且![]() ,所以
,所以![]() .
.
所以![]() ,同理
,同理![]() .
.
即![]() 解得
解得![]() ,
,
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】有一款擊鼓小游戲規則如下:每盤游戲都需要擊鼓三次,每次擊鼓要么出現一次音樂,要么不出現音樂;每盤游戲擊鼓三次后,出現一次音樂獲得10分,出現兩次音樂獲得20分,出現三次音樂獲得50分,沒有出現音樂則扣除150分(即獲得-150分).設每次擊鼓出現音樂的概率為![]() ,且各次擊鼓出現音樂相互獨立.
,且各次擊鼓出現音樂相互獨立.
(Ⅰ)玩一盤游戲,至少出現一次音樂的概率是多少?
(Ⅱ)設每盤游戲獲得的分數為![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)許多玩過這款游戲的人都發現,玩的盤數越多,分數沒有增加反而減少了.請運用概率統計的相關知識分析其中的道理.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中正確的是( )
A.若事件![]() 與事件
與事件![]() 是互斥事件,則
是互斥事件,則![]()
B.若事件![]() 與事件
與事件![]() 滿足條件:
滿足條件:![]() ,則事件A與事件
,則事件A與事件![]() 是對立事件
是對立事件
C.一個人打靶時連續射擊兩次,則事件“至少有一次中靶”與事件“至多有一次中靶”是對立事件
D.把紅、橙、黃3張紙牌隨機分給甲、乙、丙3人,每人分得1張,則事件“甲分得紅牌”與事件“乙分得紅牌”是互斥事件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量![]() (噸)與相應的生產能耗
(噸)與相應的生產能耗![]() (噸)標準煤的幾組對照數據
(噸)標準煤的幾組對照數據
|
|
|
|
|
|
|
|
|
|
(1)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)已知該廠技改前100噸甲產品的生產能耗為90噸標準煤.試根據(1)求出的線性回歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?
參考公式: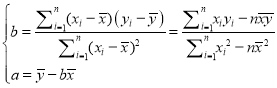
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知各項是正數的數列![]() 的前n項和為
的前n項和為![]() .
.
(1)若![]() (nN*,n≥2),且
(nN*,n≥2),且![]() .
.
①求數列![]() 的通項公式;
的通項公式;
②若![]() 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(2)數列![]() 是公比為q(q>0, q1)的等比數列,且{an}的前n項積為
是公比為q(q>0, q1)的等比數列,且{an}的前n項積為![]() .若存在正整數k,對任意nN*,使得
.若存在正整數k,對任意nN*,使得![]() 為定值,求首項
為定值,求首項![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為![]() (t為參數),以原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為
(t為參數),以原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]() ,若直線l與曲線C相交于A,B兩點,求△AOB的面積.
,若直線l與曲線C相交于A,B兩點,求△AOB的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上一點.
上一點.

(I)求證: ![]() .
.
(II)若![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點,求證:
的中點,求證: ![]() 平面
平面![]() .
.
(III)若二面角![]() 的大小為
的大小為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com