
【題目】定義函數(shù)![]() 如下:對(duì)于實(shí)數(shù)
如下:對(duì)于實(shí)數(shù)![]() ,如果存在整數(shù)
,如果存在整數(shù)![]() ,使得
,使得![]() ,則
,則![]() .則下列結(jié)論:①
.則下列結(jié)論:①![]() 是實(shí)數(shù)
是實(shí)數(shù)![]() 上的遞增函數(shù);②
上的遞增函數(shù);②![]() 是周期為1的函數(shù);③
是周期為1的函數(shù);③![]() 是奇函數(shù);④函數(shù)
是奇函數(shù);④函數(shù)![]() 的圖像與直線
的圖像與直線![]() 有且僅有一個(gè)交點(diǎn).則正確結(jié)論的序號(hào)是______.
有且僅有一個(gè)交點(diǎn).則正確結(jié)論的序號(hào)是______.
【答案】③
【解析】
直接利用對(duì)于實(shí)數(shù)![]() ,如果存在整數(shù)
,如果存在整數(shù)![]() ,使得
,使得![]() ,則
,則![]() ,對(duì)四個(gè)命題分別進(jìn)行判斷,即可得出結(jié)論.
,對(duì)四個(gè)命題分別進(jìn)行判斷,即可得出結(jié)論.
對(duì)于①如果對(duì)于實(shí)數(shù)![]() ,存在整數(shù)
,存在整數(shù)![]() ,使得
,使得![]() ,則
,則![]() ,即
,即![]() 時(shí),
時(shí),![]() ,所以
,所以![]() 在
在![]() 上為常數(shù)函數(shù),故①不正確;
上為常數(shù)函數(shù),故①不正確;
對(duì)于②令![]() ,則
,則![]() 時(shí),
時(shí),![]() ,令
,令![]() ,則
,則![]() 時(shí),
時(shí),![]() ,所以
,所以![]() ,即
,即![]() 是周期為1的函數(shù)不正確,故②不正確;
是周期為1的函數(shù)不正確,故②不正確;
對(duì)于③因?yàn)?/span>![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() 為奇函數(shù),故③正確;
為奇函數(shù),故③正確;
④由③可知,函數(shù)![]() 為奇函數(shù),又函數(shù)
為奇函數(shù),又函數(shù)![]() 也為奇函數(shù),根據(jù)奇函數(shù)的圖像關(guān)于原點(diǎn)對(duì)稱知,兩個(gè)函數(shù)的圖像如果有交點(diǎn),那么它們至少有兩個(gè)交點(diǎn),故④不正確.
也為奇函數(shù),根據(jù)奇函數(shù)的圖像關(guān)于原點(diǎn)對(duì)稱知,兩個(gè)函數(shù)的圖像如果有交點(diǎn),那么它們至少有兩個(gè)交點(diǎn),故④不正確.
綜上所述:只有③正確.
故答案為:③


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,短軸長為
,短軸長為![]() .
.
(1)求![]() 的方程;
的方程;
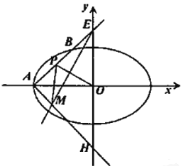
(2)如圖,經(jīng)過橢圓左頂點(diǎn)![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點(diǎn),交
兩點(diǎn),交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 為線段
為線段![]() 的中點(diǎn),若點(diǎn)
的中點(diǎn),若點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸的對(duì)稱點(diǎn)為
軸的對(duì)稱點(diǎn)為![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() (
(![]() 為坐標(biāo)原點(diǎn))垂直的直線交直線
為坐標(biāo)原點(diǎn))垂直的直線交直線![]() 于點(diǎn)
于點(diǎn)![]() ,且
,且![]() 面積為
面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若無窮數(shù)列![]() 滿足:
滿足:![]() 是正實(shí)數(shù),當(dāng)
是正實(shí)數(shù),當(dāng)![]() 時(shí),
時(shí),![]() ,則稱
,則稱![]() 是“
是“![]() —數(shù)列”.
—數(shù)列”.
(1)若![]() 是“
是“![]() —數(shù)列”且
—數(shù)列”且![]() ,寫出
,寫出![]() 的所有可能值;
的所有可能值;
(2)設(shè)![]() 是“
是“![]() —數(shù)列”,證明:
—數(shù)列”,證明:![]() 是等差數(shù)列當(dāng)且僅當(dāng)
是等差數(shù)列當(dāng)且僅當(dāng)![]() 單調(diào)遞減;
單調(diào)遞減;![]() 是等比數(shù)列當(dāng)且僅當(dāng)
是等比數(shù)列當(dāng)且僅當(dāng)![]() 單調(diào)遞增;
單調(diào)遞增;
(3)若![]() 是“
是“![]() —數(shù)列”且是周期數(shù)列(即存在正整數(shù)
—數(shù)列”且是周期數(shù)列(即存在正整數(shù)![]() ,使得對(duì)任意正整數(shù)
,使得對(duì)任意正整數(shù)![]() ,都有
,都有![]() ),求集合
),求集合![]() 的元素個(gè)數(shù)的所有可能值的個(gè)數(shù).
的元素個(gè)數(shù)的所有可能值的個(gè)數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() ,
,![]() 為正整數(shù),一個(gè)正整數(shù)數(shù)列
為正整數(shù),一個(gè)正整數(shù)數(shù)列![]() 滿足
滿足![]() .對(duì)
.對(duì)![]() ,定義集合
,定義集合![]() .數(shù)列
.數(shù)列![]() 中的
中的![]() 是集合
是集合![]() 中元素的個(gè)數(shù).
中元素的個(gè)數(shù).
(1)若數(shù)列![]() 為5,3,3,2,1,1,寫出數(shù)列
為5,3,3,2,1,1,寫出數(shù)列![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 為公比為
為公比為![]() 的等比數(shù)列,求
的等比數(shù)列,求![]() ;
;
(3)對(duì)![]() ,定義集合
,定義集合![]() ,令
,令![]() 是集合
是集合![]() 中元素?cái)?shù)的個(gè)數(shù).求證:對(duì)
中元素?cái)?shù)的個(gè)數(shù).求證:對(duì)![]() ,均有
,均有![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() .
.
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)當(dāng)![]() 時(shí),證明:
時(shí),證明:![]() ;
;
(3)求證:對(duì)任意正整數(shù)![]() ,都有
,都有![]() (其中
(其中![]() ,為自然對(duì)數(shù)的底數(shù)).
,為自然對(duì)數(shù)的底數(shù)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
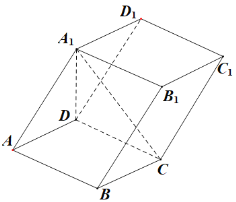
【題目】如圖,在平行六面體![]() 中,
中,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 與底面
與底面![]() 所成角為
所成角為![]() ,
,![]() .
.
(1)求證:平行六面體![]() 的體積
的體積![]() ,并求
,并求![]() 的取值范圍;
的取值范圍;
(2)若![]() ,求二面角
,求二面角![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)\![]() .
.
(1)若![]() 且
且![]() 在
在![]() 處的切線垂直于y軸,求a的值;
處的切線垂直于y軸,求a的值;
(2)若對(duì)于任意![]() ,都有
,都有![]() 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 是無窮數(shù)列,滿足
是無窮數(shù)列,滿足![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)求證:“數(shù)列![]() 中存在
中存在![]() 使得
使得![]() ”是“數(shù)列
”是“數(shù)列![]() 中有無數(shù)多項(xiàng)是
中有無數(shù)多項(xiàng)是![]() ”的充要條件;
”的充要條件;
(3)求證:在數(shù)列![]() 中
中![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】十九大以來,某貧困地區(qū)扶貧辦積極貫徹落實(shí)國家精準(zhǔn)扶貧的政策要求,帶領(lǐng)廣大農(nóng)村地區(qū)人民群眾脫貧奔小康。經(jīng)過不懈的奮力拼搏,新農(nóng)村建設(shè)取得巨大進(jìn)步,農(nóng)民年收入也逐年增加。為了更好的制定2019年關(guān)于加快提升農(nóng)民年收人力爭早日脫貧的工作計(jì)劃,該地扶貧辦統(tǒng)計(jì)了2018年![]() 位農(nóng)民的年收人并制成如下頻率分布直方圖:
位農(nóng)民的年收人并制成如下頻率分布直方圖:
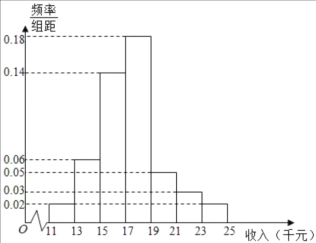
(1)根據(jù)頻率分布直方圖,估計(jì)![]() 位農(nóng)民的年平均收入
位農(nóng)民的年平均收入![]() (單位:千元)(同一組數(shù)據(jù)用該組數(shù)據(jù)區(qū)間的中點(diǎn)值表示);
(單位:千元)(同一組數(shù)據(jù)用該組數(shù)據(jù)區(qū)間的中點(diǎn)值表示);
(2)由頻率分布直方圖,可以認(rèn)為該貧困地區(qū)農(nóng)民年收入![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,其中
,其中![]() 近似為年平均收入
近似為年平均收入![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() ,經(jīng)計(jì)算得
,經(jīng)計(jì)算得![]() .利用該正態(tài)分布,求:
.利用該正態(tài)分布,求:
(i)在2019年脫貧攻堅(jiān)工作中,若使該地區(qū)約有占總農(nóng)民人數(shù)的![]() 的農(nóng)民的年收入高于扶貧辦制定的最低年收入標(biāo)準(zhǔn),則最低年收入大約為多少千元?
的農(nóng)民的年收入高于扶貧辦制定的最低年收入標(biāo)準(zhǔn),則最低年收入大約為多少千元?
(ii)為了調(diào)研“精準(zhǔn)扶貧,不落一人”的政策要求落實(shí)情況,扶貧辦隨機(jī)走訪了![]() 位農(nóng)民。若每個(gè)農(nóng)民的年收人相互獨(dú)立,問:這
位農(nóng)民。若每個(gè)農(nóng)民的年收人相互獨(dú)立,問:這![]() 位農(nóng)民中的年收入不少于
位農(nóng)民中的年收入不少于![]() 千元的人數(shù)最有可能是多少?
千元的人數(shù)最有可能是多少?
附:參考數(shù)據(jù)與公式![]()
則①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com