
【題目】如圖,三棱柱![]() 中,
中,![]() ,D為AB上一點,且
,D為AB上一點,且![]() 平面
平面![]() .
.
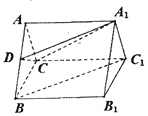
(1)求證:![]() ;
;
(2)若四邊形![]() 是矩形,且平面
是矩形,且平面![]() 平面ABC,直線
平面ABC,直線![]() 與平面ABC所成角的正切值等于2,
與平面ABC所成角的正切值等于2,![]() ,
,![]() ,求三樓柱
,求三樓柱![]() 的體積.
的體積.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在2018年俄羅斯世界杯期間,莫斯科的部分餐廳經營了來自中國的小龍蝦,這些小龍蝦標有等級代碼.為得到小龍蝦等級代碼數值![]() 與銷售單價
與銷售單價![]() 之間的關系,經統計得到如下數據:
之間的關系,經統計得到如下數據:
等級代碼數值 | 38 | 48 | 58 | 68 | 78 | 88 |
銷售單價 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
(1)已知銷售單價![]() 與等級代碼數值
與等級代碼數值![]() 之間存在線性相關關系,求
之間存在線性相關關系,求![]() 關于
關于![]() 的線性回歸方程(系數精確到0.1);
的線性回歸方程(系數精確到0.1);
(2)若莫斯科某餐廳銷售的中國小龍蝦的等級代碼數值為98,請估計該等級的中國小龍蝦銷售單價為多少元?
參考公式:對一組數據![]() ,
,![]() ,····
,····![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距最小二乘估計分別為:
的斜率和截距最小二乘估計分別為: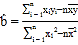 ,
,![]() .
.
參考數據:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設自然數![]() 。求證:全體不大于n的合數可重新排列(不一定按原來的大小順序排列),使得每三個依次相鄰的數都有大于1的公因數(例如,當
。求證:全體不大于n的合數可重新排列(不一定按原來的大小順序排列),使得每三個依次相鄰的數都有大于1的公因數(例如,當![]() 時,排列
時,排列![]() 就滿足要求)。
就滿足要求)。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)
已知函數![]() 是奇函數,
是奇函數,![]() 的定義域為
的定義域為![]() .當
.當![]() 時,
時,![]()
![]() .(e為自然對數的底數).
.(e為自然對數的底數).
(1)若函數![]() 在區間
在區間![]() 上存在極值點,求實數
上存在極值點,求實數![]() 的取值范圍;
的取值范圍;
(2)如果當x≥1時,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的右焦點為
的右焦點為![]() ,右頂點為
,右頂點為![]() ,設離心率為
,設離心率為![]() ,且滿足
,且滿足![]() ,其中
,其中![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)過點(0,1)的直線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點,求
兩點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種植物感染![]() 病毒極易導致死亡,某生物研究所為此推出了一種抗
病毒極易導致死亡,某生物研究所為此推出了一種抗![]() 病毒的制劑,現對20株感染了
病毒的制劑,現對20株感染了![]() 病毒的該植株樣本進行噴霧試驗測試藥效.測試結果分“植株死亡”和“植株存活”兩個結果進行統計;并對植株吸收制劑的量(單位:mg)進行統計.規定:植株吸收在6mg(包括6mg)以上為“足量”,否則為“不足量”.現對該20株植株樣本進行統計,其中 “植株存活”的13株,對制劑吸收量統計得下表.已知“植株存活”但“制劑吸收不足量”的植株共1株.
病毒的該植株樣本進行噴霧試驗測試藥效.測試結果分“植株死亡”和“植株存活”兩個結果進行統計;并對植株吸收制劑的量(單位:mg)進行統計.規定:植株吸收在6mg(包括6mg)以上為“足量”,否則為“不足量”.現對該20株植株樣本進行統計,其中 “植株存活”的13株,對制劑吸收量統計得下表.已知“植株存活”但“制劑吸收不足量”的植株共1株.
編號 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
吸收量(mg) | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 10 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
(1)完成以下![]() 列聯表,并判斷是否可以在犯錯誤概率不超過1%的前提下,認為“植株的存活”與“制劑吸收足量”有關?
列聯表,并判斷是否可以在犯錯誤概率不超過1%的前提下,認為“植株的存活”與“制劑吸收足量”有關?
吸收足量 | 吸收不足量 | 合計 | |
植株存活 | 1 | ||
植株死亡 | |||
合計 | 20 |
(2)①若在該樣本“吸收不足量”的植株中隨機抽取3株,記![]() 為“植株死亡”的數量,求
為“植株死亡”的數量,求![]() 得分布列和期望
得分布列和期望![]() ;
;
②將頻率視為概率,現在對已知某塊種植了1000株并感染了![]() 病毒的該植物試驗田里進行該藥品噴霧試驗,設“植株存活”且“吸收足量”的數量為隨機變量
病毒的該植物試驗田里進行該藥品噴霧試驗,設“植株存活”且“吸收足量”的數量為隨機變量![]() ,求
,求![]() .
.
參考數據: ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )的兩焦點與短軸的一個端點的連線構成等腰直角三角形,直線
)的兩焦點與短軸的一個端點的連線構成等腰直角三角形,直線![]() 與以橢圓C的右焦點為圓心,以橢圓的半長軸長為半徑的圓相切.
與以橢圓C的右焦點為圓心,以橢圓的半長軸長為半徑的圓相切.
(1)求橢圓C的方程;
(2)設P為橢圓C上一點,若過點![]() 的直線l與橢圓C相交于不同的兩點S和T,滿足
的直線l與橢圓C相交于不同的兩點S和T,滿足![]() (O為坐標原點),求實數t的取值范圍.
(O為坐標原點),求實數t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com