
【題目】已知橢圓![]() :
:![]() 的右焦點(diǎn)為
的右焦點(diǎn)為![]() ,右頂點(diǎn)為
,右頂點(diǎn)為![]() ,設(shè)離心率為
,設(shè)離心率為![]() ,且滿足
,且滿足![]() ,其中
,其中![]() 為坐標(biāo)原點(diǎn).
為坐標(biāo)原點(diǎn).
(1)求橢圓![]() 的方程;
的方程;
(2)過(guò)點(diǎn)(0,1)的直線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點(diǎn),求
兩點(diǎn),求![]() 面積的最大值.
面積的最大值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】
(1)設(shè)橢圓的焦半距為c,結(jié)合題意分析可得![]() ,結(jié)合橢圓的幾何性質(zhì)可得a、b的值,代入橢圓的方程即可得答案;
,結(jié)合橢圓的幾何性質(zhì)可得a、b的值,代入橢圓的方程即可得答案;
(2)由題意分析可得直線l與x軸不垂直,設(shè)其方程為y=kx+1,聯(lián)立l與橢圓C的方程,可得(4k2+3)x2+8kx﹣8=0,結(jié)合根與系數(shù)的關(guān)系可以用k表示|MN|與O到l的距離,由三角形面積公式計(jì)算可得△OMN的面積![]()
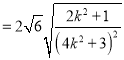 .,由基本不等式分析可得答案.
.,由基本不等式分析可得答案.
(1)設(shè)橢圓的焦半距為![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
所以![]() ,其中
,其中![]() ,又
,又![]() ,聯(lián)立解得
,聯(lián)立解得![]() ,
,![]() .
.
所以橢圓![]() 的方程是
的方程是![]() .
.
(2)由題意直線不能與![]() 軸垂直,否則將無(wú)法構(gòu)成三角形.
軸垂直,否則將無(wú)法構(gòu)成三角形.
當(dāng)直線![]() 與
與![]() 軸不垂直時(shí),設(shè)其斜率為
軸不垂直時(shí),設(shè)其斜率為![]() ,那么
,那么![]() 的方程為
的方程為![]() .
.
聯(lián)立![]() 與橢圓
與橢圓![]() 的方程,消去
的方程,消去![]() ,得
,得![]() .
.
于是直線與橢圓有兩個(gè)交點(diǎn)的充要條件是![]() ,這顯然成立.
,這顯然成立.
設(shè)點(diǎn)![]() ,
,![]() .
.
由根與系數(shù)的關(guān)系得![]() ,
,![]() .
.
所以![]()
![]() ,又
,又![]() 到
到![]() 的距離
的距離![]() .
.
所以![]() 的面
的面![]()
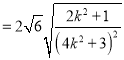 .
.
令![]() ,那么
,那么![]()
![]() ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)![]() 時(shí)取等號(hào).
時(shí)取等號(hào).
所以![]() 面積的最大值是
面積的最大值是![]() .
.


 名牌學(xué)校分層周周測(cè)系列答案
名牌學(xué)校分層周周測(cè)系列答案 黃岡海淀全程培優(yōu)測(cè)試卷系列答案
黃岡海淀全程培優(yōu)測(cè)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在△ABC中,a,b,c分別為內(nèi)角A,B,C的對(duì)邊,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面積S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】稱直角坐標(biāo)系中縱橫坐標(biāo)均為整數(shù)的 點(diǎn)為“格點(diǎn)”,稱一格點(diǎn)沿坐標(biāo)線到原點(diǎn)的最短路程為該點(diǎn)到原點(diǎn)的“格點(diǎn)距離”,格點(diǎn)距離為定值的點(diǎn)的軌跡稱為“格點(diǎn)圓”,該定值稱為格點(diǎn)圓的半徑,而每一條最短路程稱為一條半徑.當(dāng)格點(diǎn)半徑為2005時(shí),格點(diǎn)圓的半徑有________條.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某網(wǎng)紅直播平臺(tái)為確定下一季度的廣告投入計(jì)劃,收集了近6個(gè)月廣告投入量![]() (單位:萬(wàn)元)和收益
(單位:萬(wàn)元)和收益![]() (單位:萬(wàn)元)的數(shù)據(jù)如下表:
(單位:萬(wàn)元)的數(shù)據(jù)如下表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
廣告投入量/萬(wàn)元 | 2 | 4 | 6 | 8 | 10 | 12 |
收益/萬(wàn)元 | 14.21 | 20.31 | 31.8 | 31.18 | 37.83 | 44.67 |
用兩種模型①![]() ,②
,②![]() 分別進(jìn)行擬合,得到相應(yīng)的回歸方程并進(jìn)行殘差分析,得到如圖所示的殘差圖及一些統(tǒng)計(jì)量的值:
分別進(jìn)行擬合,得到相應(yīng)的回歸方程并進(jìn)行殘差分析,得到如圖所示的殘差圖及一些統(tǒng)計(jì)量的值:
|
|
|
|
7 | 30 | 1464.24 | 364 |
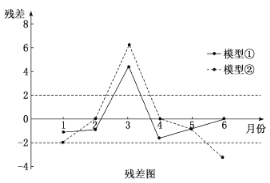
(1)根據(jù)殘差圖,比較模型①,②的擬合效果,應(yīng)選擇哪個(gè)模型?并說(shuō)明理由.
(2)殘差絕對(duì)值大于2的數(shù)據(jù)被認(rèn)為是異常數(shù)據(jù),需要剔除:
(i)剔除的異常數(shù)據(jù)是哪一組?
(ii)剔除異常數(shù)據(jù)后,求出(1)中所選模型的回歸方程;
(iii)廣告投入量![]() 時(shí),(ii)中所得模型收益的預(yù)報(bào)值是多少?
時(shí),(ii)中所得模型收益的預(yù)報(bào)值是多少?
附:對(duì)于一組數(shù)據(jù)![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計(jì)分別為:
的斜率和截距的最小二乘估計(jì)分別為: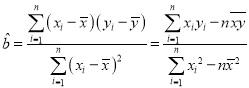 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,三棱柱![]() 中,
中,![]() ,D為AB上一點(diǎn),且
,D為AB上一點(diǎn),且![]() 平面
平面![]() .
.
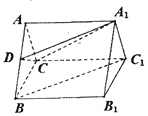
(1)求證:![]() ;
;
(2)若四邊形![]() 是矩形,且平面
是矩形,且平面![]() 平面ABC,直線
平面ABC,直線![]() 與平面ABC所成角的正切值等于2,
與平面ABC所成角的正切值等于2,![]() ,
,![]() ,求三樓柱
,求三樓柱![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖設(shè)計(jì)一幅矩形宣傳畫(huà),要求畫(huà)面面積為4840![]() ,畫(huà)面上下邊要留8cm空白,左右要留5cm空白,怎樣確定畫(huà)面高與寬的尺寸,才能使宣傳畫(huà)所用紙張面積最小?
,畫(huà)面上下邊要留8cm空白,左右要留5cm空白,怎樣確定畫(huà)面高與寬的尺寸,才能使宣傳畫(huà)所用紙張面積最小?

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求該函數(shù)的值域;
時(shí),求該函數(shù)的值域;
(2)求不等式![]() 的解集;
的解集;
(3)若![]() 對(duì)于
對(duì)于![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】建造一條防洪堤,其斷面為等腰梯形,腰與底邊成角為![]() ,防洪堤高記為
,防洪堤高記為![]() (如圖),考慮到防洪堤堅(jiān)固性及石塊用料等因素,設(shè)計(jì)其斷面面積為
(如圖),考慮到防洪堤堅(jiān)固性及石塊用料等因素,設(shè)計(jì)其斷面面積為![]() 平方米,為了使堤的上面與兩側(cè)面的水泥用料最省,則斷面的外周長(zhǎng)
平方米,為了使堤的上面與兩側(cè)面的水泥用料最省,則斷面的外周長(zhǎng)![]() (
(![]() )要最小.
)要最小.

(1)用![]() 表示
表示![]() 、
、![]() ;
;
(2)將![]() 表示成
表示成![]() 的函數(shù)
的函數(shù)![]() ,如
,如![]() 限制在
限制在![]() 范圍內(nèi),
范圍內(nèi),![]() 最小為多少米?并說(shuō)明理由.
最小為多少米?并說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在如圖所示的空間幾何體中,平面![]() 平面
平面![]() ,
,![]() 與
與![]() 是邊長(zhǎng)為2的等邊三角形,
是邊長(zhǎng)為2的等邊三角形,![]() ,BE和平面ABC所成的角為
,BE和平面ABC所成的角為![]() ,且點(diǎn)E在平面ABC上的射影落在
,且點(diǎn)E在平面ABC上的射影落在![]() 的平分線上.
的平分線上.

(1)求證:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com