
【題目】已知函數![]() .
.
(1)若函數![]() 的圖象在點
的圖象在點![]() 處的切線方程為
處的切線方程為![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)當![]() 時,在區間
時,在區間![]() 上至少存在一個
上至少存在一個![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)m=2,n=﹣1;(2)![]() .
.
【解析】分析:(1)求出函數的導數,結合切點坐標求出![]() ,
,![]() 的值即可;
的值即可;
(2)求出函數的導數,通過討論m的范圍,求出函數的單調區間,從而求出m的范圍即可.
詳解:(1)∵f′(x)=﹣![]() +n,
+n,
故f′(0)=n﹣m,即n﹣m=﹣3,
又∵f(0)=m,故切點坐標是(0,m),
∵切點在直線y=﹣3x+2上,
故m=2,n=﹣1;
(2)∵f(x)=![]() +x,∴f′(x)=
+x,∴f′(x)=![]() ,
,
當m≤0時,f′(x)>0,
故函數f(x)在(﹣∞,1)遞增,
令x0=a<0,此時f(x)<0,符合題意,
當m>0時,即0<m<e時,則函數f(x)在(﹣∞,lnm)遞減,在(lnm,+∞)遞增,
①當lnm<1即0<m<e時,則函數f(x)在(﹣∞,lnm)遞減,在(lnm,1]遞增,
f(x)min=f(lnm)=lnm+1<0,解得:0<m<![]() ,
,
②當lnm>1即m≥e時,函數f(x)在區間(﹣∞,1)遞減,
則函數f(x)在區間(﹣∞,1)上的最小值是f(1)=![]() +1<0,解得:m<﹣e,無解,
+1<0,解得:m<﹣e,無解,
綜上,m<![]() ,即m的范圍是(﹣∞,
,即m的范圍是(﹣∞,![]() ).
).


科目:高中數學 來源: 題型:
【題目】已知數列{an}中,a1=1,an+1=an+n,利用如圖所示的程序框圖計算該數列的第10項,則判斷框中應填的語句是( ) 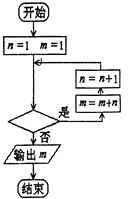
A.n>10
B.n≤10
C.n<9
D.n≤9
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分) 某居民小區有兩個相互獨立的安全防范系統(簡稱系統)![]() 和
和![]() ,系統
,系統![]() 和
和![]() 在任意時刻發生故障的概率分別為
在任意時刻發生故障的概率分別為![]() 和
和![]() 。
。
(Ⅰ)若在任意時刻至少有一個系統不發生故障的概率為![]() ,求
,求![]() 的值;
的值;
(Ⅱ)設系統![]() 在3次相互獨立的檢測中不發生故障的次數為隨機變量
在3次相互獨立的檢測中不發生故障的次數為隨機變量![]() ,求
,求![]() 的概率分布列及數學期望
的概率分布列及數學期望![]() 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國北斗衛星導航系統是中國自行研制的全球衛星導航系統,作為國家戰略性空間基礎設施,我國北斗衛星導航系統不僅對國防安全意義重大,而且在民用領域的精準化應用也越來越廣泛.據統計,2016年衛星導航與位置服務產業總產值達到2118億元,較2015年約增長![]() .下面是40個城市北斗衛星導航系統與位置服務產業的產值(單位:萬元)的頻率分布直方圖:
.下面是40個城市北斗衛星導航系統與位置服務產業的產值(單位:萬元)的頻率分布直方圖:
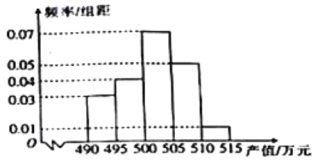
(1)根據頻率分布直方圖,求產值小于500萬元的城市個數;
(2)在上述抽取的40個城市中任取2個,設![]() 為產值不超過500萬元的城市個數,求
為產值不超過500萬元的城市個數,求![]() 的分布列及期望和方差.
的分布列及期望和方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某快餐連鎖店招聘外賣騎手,該快餐連鎖店提供了兩種日工資方案:方案(1)規定每日底薪50元,快遞業務每完成一單提成3元;方案(2)規定每日底薪100元,快遞業務的前44單沒有提成,從第45單開始,每完成一單提成5元.該快餐連鎖店記錄了每天騎手的人均業務量.現隨機抽取100天的數據,將樣本數據分為[ 25,35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95]七組,整理得到如圖所示的頻率分布直方圖。

(1)隨機選取一天,估計這一天該連鎖店的騎手的人均日快遞業務量不少于65單的概率;
(2)若騎手甲、乙選擇了日工資方案(1),丙、丁選擇了日工資方案(2).現從上述4名騎手中隨機選取2人,求至少有1名騎手選擇方案(1)的概率;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】統計表明某型號汽車在勻速行駛中每小時的耗油量![]() (升)關于行駛速度
(升)關于行駛速度![]() (千米/小時)的函數為
(千米/小時)的函數為![]()
![]() .
.
(1)當![]() 千米/小時時,行駛
千米/小時時,行駛![]() 千米耗油量多少升?
千米耗油量多少升?
(2)若油箱有![]() 升油,則該型號汽車最多行駛多少千米?
升油,則該型號汽車最多行駛多少千米?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com