
【題目】已知函數![]()
![]() 在區間
在區間![]() 上的最大值為
上的最大值為![]() ,最小值為
,最小值為![]() ,記
,記![]() ,
,![]() ;
;
(1)求實數![]() 、
、![]() 的值;
的值;
(2)若不等式![]() 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的范圍;
的范圍;
(3)對于定義在![]() 上的函數
上的函數![]() ,設
,設![]() ,
,![]() ,用任意
,用任意![]()
![]() 將
將![]() 劃分成
劃分成![]() 個小區間,其中
個小區間,其中![]() ,若存在一個常數
,若存在一個常數![]() ,使得不等式
,使得不等式![]() 恒成立,則稱函數
恒成立,則稱函數![]() 為在
為在![]() 上的有界變差函數,試證明函數
上的有界變差函數,試證明函數![]() 是在
是在![]() 上的有界變差函數,并求出
上的有界變差函數,并求出![]() 的最小值;
的最小值;
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)證明見解析,
;(3)證明見解析,![]() ;
;
【解析】
(1)由已知![]() 在區間
在區間![]() 上的最大值為4,最小值為1,結合函數的單調性及最值,易構造關于
上的最大值為4,最小值為1,結合函數的單調性及最值,易構造關于![]() 的方程組,解得
的方程組,解得![]() 的值。
的值。
(2)求出![]() ,
,![]() 對任意
對任意![]() 恒成立等價于
恒成立等價于![]() 恒成立,求實數
恒成立,求實數![]() 的范圍。
的范圍。
(3)根據有界變差函數的定義,我們先將區間![]() 進行劃分,進而判斷
進行劃分,進而判斷![]() 是否恒成立,進而得到結論。
是否恒成立,進而得到結論。
(1)因為![]() ,因為
,因為![]() ,對稱軸
,對稱軸![]()
所以![]() 在區間
在區間![]() 上是增函數,
上是增函數,
又函數![]()
![]() 在區間
在區間![]() 上的最大值為
上的最大值為![]() ,最小值為
,最小值為![]()
所以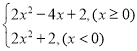
解得:![]()
所以![]()
故實數![]()
(2)由(1)可知![]()
因為![]() ,所以
,所以![]()
因為![]() 對任意
對任意![]() 恒成立,
恒成立,
令![]()
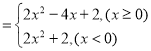
根據二次函數的圖像和性質可得:![]()
則![]()
令![]() ,則
,則![]()
解得:![]()
即![]()
所以![]()
(3)函數![]() 為
為![]() 上的有界變差函數,又
上的有界變差函數,又![]() 為
為![]() 上的單增函數,
上的單增函數,
且對任意劃分![]()
有![]()
所以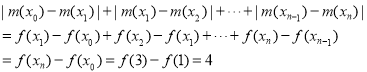
所以存在常數M使得![]() 恒成立,即
恒成立,即![]()


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)設點![]() 分別為曲線
分別為曲線![]() 與曲線
與曲線![]() 上的任意一點,求
上的任意一點,求![]() 的最大值;
的最大值;
(2)設直線![]() (
(![]() 為參數)與曲線
為參數)與曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高鐵是一種快捷的交通工具,為我們的出行提供了極大的方便。某高鐵換乘站設有編號為①,②,③,④,⑤的五個安全出口,若同時開放其中的兩個安全出口,疏散![]() 名乘客所需的時間如下:
名乘客所需的時間如下:
安全出口編號 | ①② | ②③ | ③④ | ④⑤ | ①⑤ |
疏散乘客時間(s) | 120 | 220 | 160 | 140 | 200 |
則疏散乘客最快的一個安全出口的編號是( )
A. ①B. ②C. ④D. ⑤
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xsinx的圖象是下列兩個圖象中的一個,如圖,請你選擇后再根據圖象作出下面的判斷:若x1,x2∈(![]() ),且f(x1)<f(x2),則( )
),且f(x1)<f(x2),則( )
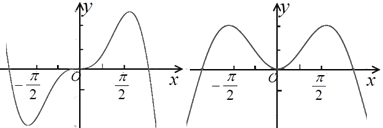
A.x1>x2B.x1+x2>0C.x1<x2D.x12<x22
查看答案和解析>>
科目:高中數學 來源: 題型:
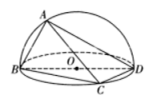
【題目】如圖,已知![]() 是圓
是圓![]() 的直徑,
的直徑,![]() ,
,![]() 在圓上且分別在
在圓上且分別在![]() 的兩側,其中
的兩側,其中![]() ,
,![]() .現將其沿
.現將其沿![]() 折起使得二面角
折起使得二面角![]() 為直二面角,則下列說法不正確的是( )
為直二面角,則下列說法不正確的是( )
A.![]() ,
,![]() ,
,![]() ,
,![]() 在同一個球面上
在同一個球面上
B.當![]() 時,三棱錐
時,三棱錐![]() 的體積為
的體積為![]()
C.![]() 與
與![]() 是異面直線且不垂直
是異面直線且不垂直
D.存在一個位置,使得平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,“大衍數列”:0,2,4,8,12….來源于《乾坤譜》中對《易傳》“大衍之數五十”的推論,主要用于解釋中國傳統文化中的太極衍生過程中曾經經歷過的兩儀數量總和.下圖是求大衍數列前![]() 項和的程序框圖.執行該程序框圖,輸入
項和的程序框圖.執行該程序框圖,輸入![]() ,則輸出的
,則輸出的![]() ( )
( )
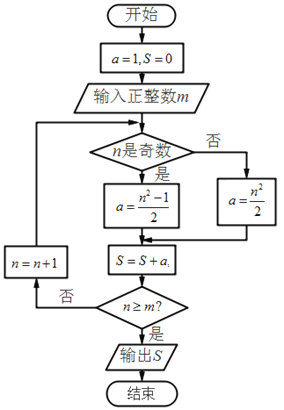
A.100B.140C.190D.250
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com