考點:異面直線及其所成的角,點、線、面間的距離計算
專題:空間位置關系與距離,空間角
分析:(I)利用三角形的中位線定理和正方體的性質即可證明;
(II)利用正方體的性質、等邊三角形的性質和異面直線所成的角即可得出;
(III)利用點到直線的距離公式即可得出.
解答:
(I)證明:在△ABC中,∵點E,F分別為棱AB,BC的中點,∴EF∥AC.
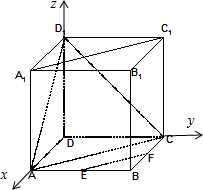
由正方體的性質可知:對角面ACC
1A
1為矩形,∴AC∥A
1C
1,
∴EF∥A
1C
1.
(Ⅱ)解:又正方體的性質可得△ACD
1為等邊三角形,
∴∠CAD
1=60°.
由(I)可知:∠CAD
1即為異面直線EF與AD
1所成的角.
因此異面直線EF與AD
1所成角為60°.
(Ⅲ)解:如圖所示,建立空間直角坐標系.
則A(2,0,0),C(0,2,0),D
1(0,0,2),E(2,1,0).
∴
=(-2,2,0),
=(-2,0,2),
=(0,1,0).
設平面ACD
1的法向量
=(x,y,z),
則
,令x=1,則y=z=1.
∴
=(1,1,1).
∴點E到平面AD
1C的距離d=
=
=
.
點評:本題綜合考查了三角形的中位線定理、正方體的性質、等邊三角形的性質、異面直線所成的角、點到直線的距離公式等基礎知識與基本技能方法,考查了推理能力和計算能力,考查了空間想象能力,屬于中檔題.

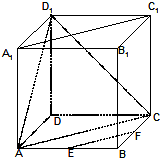 如圖,棱長為2的正方體ABCD-A1B1C1D1中,點E,F分別為棱AB,BC的中點.
如圖,棱長為2的正方體ABCD-A1B1C1D1中,點E,F分別為棱AB,BC的中點. 

