
【題目】2017年5月,來自“一帶一路”沿線的20國青年評選出了中國的“新四大發明”:高鐵、掃碼支付、共享單車和網購。為拓展市場,某調研組對甲、乙兩個品牌的共享單車在5個城市的用戶人數進行統計,得到如下數據:
城市 品牌 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
甲品牌(百萬) | 4 | 3 | 8 | 6 | 12 |
乙品牌(百萬) | 5 | 7 | 9 | 4 | 3 |
(Ⅰ)如果共享單車用戶人數超過5百萬的城市稱為“優質潛力城市”,否則“非優”,請據此判斷是否有85%的把握認為“優質潛力城市”與共享單車品牌有關?
(Ⅱ)如果不考慮其它因素,為拓展市場,甲品牌要從這5個城市中選出3個城市進行大規模宣傳.
①在城市Ⅰ被選中的條件下,求城市Ⅱ也被選中的概率;
②以![]() 表示選中的城市中用戶人數超過5百萬的個數,求隨機變量
表示選中的城市中用戶人數超過5百萬的個數,求隨機變量![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
下面臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式: K2=![]() ,n=a+b+c+d
,n=a+b+c+d
【答案】(1)沒有85%的理由(2)①![]() ,②見解析
,②見解析
【解析】試題分析:(Ⅰ)先列出列聯表,然后根據公式求出![]() ,與臨界值比較即可得結果;(Ⅱ)①令事件
,與臨界值比較即可得結果;(Ⅱ)①令事件![]() 為“城市I被選中”;事件
為“城市I被選中”;事件![]() 為“城市II被選中”,
為“城市II被選中”,
則![]() ,由條件概率公式可得結果;②隨機變量
,由條件概率公式可得結果;②隨機變量![]() 的所有可能取值為
的所有可能取值為![]() , 根據古典概型概率公式結合組合知識求出各隨機變量對應的概率,從而可得分布列,進而利用期望公式可得
, 根據古典概型概率公式結合組合知識求出各隨機變量對應的概率,從而可得分布列,進而利用期望公式可得![]() 的數學期望.
的數學期望.
試題解析:(Ⅰ)根據題意列出![]() 列聯表如下:
列聯表如下:
優質城市 單車品牌 | 優質城市 | 非優質城市 | 合計 |
甲品牌(個) | 3 | 2 | 5 |
乙品牌(個) | 2 | 3 | 5 |
合計 | 5 | 5 | 10 |
![]() ,
,
所以沒有85%的把握認為“優質潛力城市”與“共享單車”品牌有關.
(Ⅱ)①令事件![]() 為“城市I被選中”;事件
為“城市I被選中”;事件![]() 為“城市II被選中”,
為“城市II被選中”,
則![]() ,
,
所以![]() .
.
②隨機變量![]() 的所有可能取值為
的所有可能取值為![]() ,
, ![]() ;
;![]() ;
;
![]() .故
.故![]() 的分布列為
的分布列為
| 1 | 2 | 3 |
|
|
|
|
![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex-x2+a,x∈R的圖象在x=0處的切線方程為y=bx.(e≈2.718 28)
(1)求函數f(x)的解析式;
(2)當x∈R時,求證:f(x)≥-x2+x;
(3)若f(x)>kx對任意的x∈(0,+∞)恒成立,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017吉林延邊州模擬)已知在△ABC中,B(-1,0),C(1,0),且|AB|+|AC|=4.
(1)求動點A的軌跡M的方程;
(2)P為軌跡M上的動點,△PBC的外接圓為☉O1,當點P在軌跡M上運動時,求點O1到x軸的距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于下列四個命題:
p1:x0∈(0,+∞),![]() ;
;
p2:x0∈(0,1),lo![]() x0>lo
x0>lo![]() x0;
x0;
p3:x∈(0,+∞),![]() <lo
<lo![]() x;
x;
p4:x∈![]() <lo
<lo![]() x.
x.
其中的真命題是( )
A. p1,p3 B. p1,p4
C. p2,p3 D. p2,p4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 有極值,且導函數
有極值,且導函數![]() 的極值點是
的極值點是![]() 的零點.
的零點.
(1)求![]() 關于
關于![]() 的函數關系式,并寫出定義域;
的函數關系式,并寫出定義域;
(2)證明:![]() ;
;
(3)若![]() ,這兩個函數的所有極值之和不小于
,這兩個函數的所有極值之和不小于![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,以
中,以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的方程是
的方程是![]() ,將
,將![]() 向上平移2個單位得到曲線
向上平移2個單位得到曲線![]() .
.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)直線![]() 的參數方程為
的參數方程為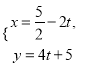 (
(![]() 為參數),判斷直線
為參數),判斷直線![]() 與曲線
與曲線![]() 的位置關系.
的位置關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市民用水擬實行階梯水價,每人用水量中不超過![]() 立方米的部分按4元/立方米收費,超出
立方米的部分按4元/立方米收費,超出![]() 立方米的部分按10元/立方米收費,從該市隨機調查了10000位居民,獲得了他們某月的用水量數據,整理得到如下頻率分布直方圖:
立方米的部分按10元/立方米收費,從該市隨機調查了10000位居民,獲得了他們某月的用水量數據,整理得到如下頻率分布直方圖:
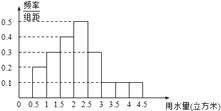
(1)如果![]() 為整數,那么根據此次調查,為使80%以上居民在該月的用水價格為4元/立方米,
為整數,那么根據此次調查,為使80%以上居民在該月的用水價格為4元/立方米, ![]() 至少定為多少?
至少定為多少?
(2)假設同組中的每個數據用該組區間的右端點值代替,當![]() 時,估計該市居民該月的人均水費.
時,估計該市居民該月的人均水費.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個幾何體的三視圖如圖所示(單位:m),則該幾何體的表面積為(單位:m2)( )
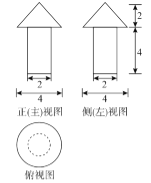
A. (11+4![]() )π B. (12+4
)π B. (12+4![]() )π C. (13+4
)π C. (13+4![]() )π D. (14+4
)π D. (14+4![]() )π
)π
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com