
【題目】已知函數(shù)![]() ,若對任意的
,若對任意的![]() 且
且![]() ,都有
,都有![]() ,則實數(shù)
,則實數(shù)![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
將x1f(x1)+x2f(x2)≥x1f(x2)+x2f(x1)變形得[f(x1)﹣f(x2)(x1﹣x2)≥0,進而分析函數(shù)f(x)![]() 為增函數(shù)或常數(shù)函數(shù),據(jù)此可得答案.
為增函數(shù)或常數(shù)函數(shù),據(jù)此可得答案.
根據(jù)題意,將x1f(x1)+x2f(x2)≥x1f(x2)+x2f(x1)變形可得[f(x1)﹣f(x2)]
(x1﹣x2)≥0,所以函數(shù)f(x)![]() 為增函數(shù)或常數(shù)函數(shù).
為增函數(shù)或常數(shù)函數(shù).
當(dāng)f(x)![]() 為增函數(shù)時,則f
為增函數(shù)時,則f![]() (x)=x
(x)=x![]() -3kx
-3kx![]() -x
-x![]()
![]() ,
,
所以3k![]() ,h(x)=
,h(x)= ![]() ,
,
h![]() (x)=
(x)=![]() >0,
>0,![]() h(x)
h(x)![]() 為增函數(shù),
為增函數(shù),
x![]() , h(x)
, h(x)![]() 1
1 ![]() 3k
3k![]() , k
, k![]() .
.
因為f(x)![]() 不可能為常數(shù)函數(shù),(舍) 所以k
不可能為常數(shù)函數(shù),(舍) 所以k![]() .
.
故選:D


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,對稱軸為直線![]() 的拋物線經(jīng)過點
的拋物線經(jīng)過點![]() 和
和![]() .
.
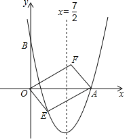
(1)求拋物線解析式及頂點坐標;
(2)設(shè)點![]() 是拋物線上一動點,且位于第四象限,四邊形OEAF是以OA為對角線的平行四邊形,求四邊形OEAF的面積S與x之間的函數(shù)關(guān)系式,并寫出自變量x的取值范圍;
是拋物線上一動點,且位于第四象限,四邊形OEAF是以OA為對角線的平行四邊形,求四邊形OEAF的面積S與x之間的函數(shù)關(guān)系式,并寫出自變量x的取值范圍;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為調(diào)查某社區(qū)居民的業(yè)余生活狀況,研究這一社區(qū)居民在20:00-22:00時間段的休閑方式與性別的關(guān)系,隨機調(diào)查了該社區(qū)80人,得到下面的數(shù)據(jù)表:
休閑方式 性別 | 看電視 | 看書 | 合計 |
男 | 10 | 50 | 60 |
女 | 10 | 10 | 20 |
合計 | 20 | 60 | 80 |
(1)根據(jù)以上數(shù)據(jù),能否有![]() 的把握認為“在20:00-22:00時間段的休閑方式與性別有關(guān)系”?
的把握認為“在20:00-22:00時間段的休閑方式與性別有關(guān)系”?
(2)將此樣本的頻率估計為總體的概率,隨機調(diào)查3名在該社區(qū)的男性,設(shè)調(diào)查的3人在這一時間段以看書為休閑方式的人數(shù)為隨機變量![]() ,求
,求![]() 的數(shù)學(xué)期望和方差.
的數(shù)學(xué)期望和方差.
參考公式與數(shù)據(jù)![]() 對應(yīng)
對應(yīng)![]() ,
,![]() 對應(yīng)
對應(yīng)![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
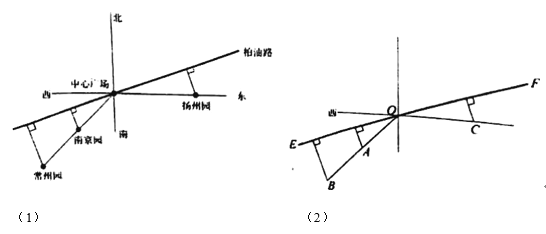
【題目】江蘇省園博會有一中心廣場,南京園,常州園都在中心廣場的南偏西45°方向上,到中心廣場的距離分別為![]() km,
km,![]() km;揚州園在中心廣場的正東方向,到中心廣場的距離為
km;揚州園在中心廣場的正東方向,到中心廣場的距離為![]() km.規(guī)劃建設(shè)一條筆直的柏油路穿過中心廣場,且將南京園,常州園,揚州園到柏油路的最短路徑鋪設(shè)成鵝卵石路(如圖(1)、(2)).已知鋪設(shè)每段鵝卵石路的費用(萬元)與其長度的平方成正比,比例系數(shù)為2.設(shè)柏油路與正東方向的夾角,即圖(2)中∠COF為
km.規(guī)劃建設(shè)一條筆直的柏油路穿過中心廣場,且將南京園,常州園,揚州園到柏油路的最短路徑鋪設(shè)成鵝卵石路(如圖(1)、(2)).已知鋪設(shè)每段鵝卵石路的費用(萬元)與其長度的平方成正比,比例系數(shù)為2.設(shè)柏油路與正東方向的夾角,即圖(2)中∠COF為![]() (
(![]() (0,
(0,![]() )),鋪設(shè)三段鵝卵石路的總費用為y(萬元).
)),鋪設(shè)三段鵝卵石路的總費用為y(萬元).
(1)求南京園到柏油路的最短距離![]() 關(guān)于
關(guān)于![]() 的表達式;
的表達式;
(2)求y的最小值及此時tan![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在底面是菱形的四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 在
在![]() 上,且
上,且![]() .
.

(1)點![]() 在棱
在棱![]() 上且
上且![]() 平面
平面![]() ,求線段
,求線段![]() 的長度;
的長度;
(2)在(1)的條件下,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知常數(shù)![]() ,函數(shù)
,函數(shù)![]() .
.
(1)討論![]() 在區(qū)間
在區(qū)間![]() 上的單調(diào)性;
上的單調(diào)性;
(2)若![]() 存在兩個極值點
存在兩個極值點![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]()
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的極值.
的極值.
(2)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上有唯一的零點,求實數(shù)
上有唯一的零點,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
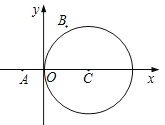
【題目】如圖,在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 及點
及點![]() ,
,![]() .
.
(1)若直線![]() 平行于
平行于![]() ,與圓
,與圓![]() 相交于
相交于![]() ,
,![]() 兩點,
兩點,![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)在圓![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ?若存在,求點
?若存在,求點![]() 的個數(shù);若不存在,說明理由.
的個數(shù);若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知扇形的圓心角∠AOB=![]() ,半徑為
,半徑為![]() ,若點C是
,若點C是![]() 上的一動點(不與點A,B重合).
上的一動點(不與點A,B重合).

(1)若弦![]() ,求
,求![]() 的長;
的長;
(2)求四邊形OACB面積的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com