
【題目】為推行“新課堂”教學法,某化學老師分別用傳統教學和“新課堂”兩種不同的教學方式,在甲、乙兩個平行班進行教學實驗,為了解教學效果,期中考試后,分別從兩個班級中各隨機抽取![]() 名學生的成績進行統計,作出的莖葉圖如下圖,記成績不低于
名學生的成績進行統計,作出的莖葉圖如下圖,記成績不低于![]() 分者為“成績優良”.
分者為“成績優良”.

(1)分別計算甲、乙兩班![]() 個樣本中,化學分數前十的平均分,并據此判斷哪種教學方式的教學效果更
個樣本中,化學分數前十的平均分,并據此判斷哪種教學方式的教學效果更
佳;
(2)甲、乙兩班![]() 個樣本中,成績在
個樣本中,成績在![]() 分以下(不含
分以下(不含![]() 分)的學生中任意選取
分)的學生中任意選取![]() 人,求這
人,求這![]() 人來自不同班級的概率;
人來自不同班級的概率;
(3)由以上統計數據填寫下面![]() 列聯表,并判斷能否在犯錯誤的概率不超過
列聯表,并判斷能否在犯錯誤的概率不超過![]() 的前提下認為“成績優良與教學方式有關”?
的前提下認為“成績優良與教學方式有關”?
甲班 | 乙班 | 總計 | |
成績優良 | |||
成績不優良 | |||
總計 |
附: 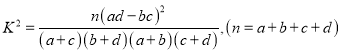
獨立性檢驗臨界值表:
|
|
|
|
|
|
|
|
|
|
【答案】(1)高效課堂更佳;(2) ![]() ;(3)能.
;(3)能.
【解析】試題分析:(1)由題意,可根據莖葉圖所提供數據,對甲乙兩個班各取前10名的分數,并計算其平均值即可,由此可判斷高效課堂更佳;(2)由莖葉圖統計兩個班60分以下的人數,再按古典概型概率的計算公式進行運算即可;(3)根據題意,由莖葉圖統計列聯表中的人數,根據公式算出![]() ,再比對臨界值表,從而可得出結論.
,再比對臨界值表,從而可得出結論.
試題解析:(1)甲班樣本化學成績前十的平均分為
![]() ;
;
乙班樣本化學成績前十的平均分為
![]() ;
;
甲班樣本化學成績前十的平均分遠低于乙班樣本化學成績前十的平均分,大致可以判斷“高效課堂”教學方式的教學效果更佳.
(2)樣本中成績![]() 分以下的學生中甲班有
分以下的學生中甲班有![]() 人,記為:
人,記為: ![]() ,乙班有
,乙班有![]() 人,記為:
人,記為: ![]() .
.
則從![]() ,
, ![]() 六個元素中任意選
六個元素中任意選![]() 個的所有基本事件如下:
個的所有基本事件如下:
![]() ,一共有
,一共有![]() 個基本事件,
個基本事件,
設![]() 表示“這
表示“這![]() 人來自不同班級”有如下:
人來自不同班級”有如下:
![]() ,一共有
,一共有![]() 個基本事件,
個基本事件,
所以![]() .
.
(3)
甲班 | 乙班 | 總計 | |
成績優良 |
|
|
|
成績不優良 |
|
|
|
總計 |
|
|
|
根據![]() 列聯表中的數據,得
列聯表中的數據,得![]() 的觀測值為
的觀測值為
![]() ,
,
∴能在犯錯誤的概率不超過![]() 的前提下認為“成績優良與教學方式有關”.
的前提下認為“成績優良與教學方式有關”.


 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:高中數學 來源: 題型:
【題目】函數![]() 的部分圖像如圖所示,將
的部分圖像如圖所示,將![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后得到函數
個單位長度后得到函數![]() 的圖象.
的圖象.
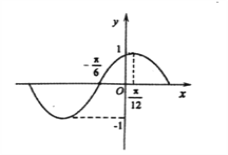
(1)求函數![]() 的解析式;
的解析式;
(2)在![]() 中,角A,B,C滿足
中,角A,B,C滿足![]() ,且其外接圓的半徑R=2,求
,且其外接圓的半徑R=2,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有以下命題:
①對任意的α∈R都有sin3α=3sinα﹣4sin3α成立;
②對任意的△ABC都有等式a=bcosA+ccosB成立;
③滿足“三邊是連續的三個正整數且最大角是最小的2倍”的三角形存在且唯一;
④若A,B是鈍角△ABC的二銳角,則sinA+sinB<cosA+cosB.
其中正確的命題的個數是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心為原點
的中心為原點![]() ,離心率
,離心率![]() ,其中一個焦點的坐標為
,其中一個焦點的坐標為![]()
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)當點![]() 在橢圓
在橢圓![]() 上運動時,設動點
上運動時,設動點![]() 的運動軌跡為
的運動軌跡為![]() 若點
若點![]() 滿足:
滿足: ![]() 其中
其中![]() 是
是![]() 上的點.直線
上的點.直線![]() 的斜率之積為
的斜率之積為![]() ,試說明:是否存在兩個定點
,試說明:是否存在兩個定點![]() ,使得
,使得![]() 為定值?若存在,求
為定值?若存在,求![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有兩個不透明的箱子,每個箱子都裝有4個完全相同的小球,球上分別標有數字1,2,3,4.
(1)甲從其中一個箱子中摸出一個球,乙從另一個箱子摸出一個球,誰摸出的球上標的數字大誰就獲勝(若數字相同則為平局),求甲獲勝的概率;
(2)摸球方法與(1)同,若規定:兩人摸到的球上所標數字相同甲獲勝,所標數字不相同則乙獲勝,這樣規定公平嗎?請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一架飛機以600km/h的速度,沿方位角60°的航向從A地出發向B地飛行,飛行了36min后到達E地,飛機由于天氣原因按命令改飛C地,已知AD=600 ![]() km,CD=1200km,BC=500km,且∠ADC=30°,∠BCD=113°.問收到命令時飛機應該沿什么航向飛行,此時E地離C地的距離是多少?(參考數據:tan37°=
km,CD=1200km,BC=500km,且∠ADC=30°,∠BCD=113°.問收到命令時飛機應該沿什么航向飛行,此時E地離C地的距離是多少?(參考數據:tan37°= ![]() )
) 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某興趣小組欲研究晝夜溫差大小與患感冒人數多少之間的關系,他們分別到氣象局與某醫院抄錄了 1至6月份每月10號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
晝夜溫差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就診人數y(個) | 22 | 25 | 29 | 26 | 16 | 12 |
該興趣小組確定的研究方案是:先從這六組數據中選取2組,用剩下的4組數據求線性回歸方程,再用被選取的2組數據進行檢驗.
(1)求選取的2組數據恰好是相鄰兩個月的概率;
(2)若選取的是1月與6月的兩組數據,請根據2至5月份的數據,求出y關于x的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2人,則認為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?
(參考:用最小二乘法求線性回歸方程系數公式 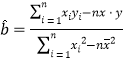 ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin2x﹣ ![]() cos2x
cos2x
(1)求函數的最小正周期及函數圖象的對稱中心;
(2)若不等式﹣2<f(x)﹣m<2在x∈[ ![]() ]上恒成立,求實數m的取值范圍.
]上恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com