
【題目】設(shè)全集U=R,集合A={x|﹣1≤x<3},B={x|2x﹣4≥x﹣2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},滿足B∪C=C,求實數(shù)a的取值范圍.
【答案】
(1)解:由集合B中的不等式2x﹣4≥x﹣2,解得x≥2,
∴B={x|x≥2},又A={x|﹣1≤x<3},
∴A∩B={x|2≤x<3},又全集U=R,
∴U(A∩B)={x|x<2或x≥3}
(2)解:由集合C中的不等式2x+a>0,解得x>﹣ ![]() ,
,
∴C={x|x>﹣ ![]() },
},
∵B∪C=C,
∴BC,
∴﹣ ![]() <2,解得a>﹣4;
<2,解得a>﹣4;
故a的取值范圍為(﹣4,+∞)
【解析】(1)求出集合B中不等式的解集確定出集合B,求出集合A與集合B的公共解集即為兩集合的交集,根據(jù)全集為R,求出交集的補集即可;(2)求出集合C中的不等式的解集,確定出集合C,由B與C的并集為集合C,得到集合B為集合C的子集,即集合B包含于集合C,從而列出關(guān)于a的不等式,求出不等式的解集即可得到a的范圍.


科目:高中數(shù)學 來源: 題型:
【題目】已知向量![]() =(2cos
=(2cos![]() ,
, ![]() sin
sin![]() ),
),![]() =(cos
=(cos![]() ,2cos
,2cos![]() ),(ω>0),設(shè)函數(shù)f(x)=
),(ω>0),設(shè)函數(shù)f(x)=![]()
![]() ,且f(x)的最小正周期為π.
,且f(x)的最小正周期為π.
(1)求函數(shù)f(x)的表達式;
(2)求f(x)的單調(diào)遞增區(qū)間.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】甲、乙兩企業(yè)生產(chǎn)同一種型號零件,按規(guī)定該型號零件的質(zhì)量指標值落在![]() 內(nèi)為優(yōu)質(zhì)品.從兩個企業(yè)生產(chǎn)的零件中各隨機抽出了500件,測量這些零件的質(zhì)量指標值,得結(jié)果如下表:
內(nèi)為優(yōu)質(zhì)品.從兩個企業(yè)生產(chǎn)的零件中各隨機抽出了500件,測量這些零件的質(zhì)量指標值,得結(jié)果如下表:
甲企業(yè):

乙企業(yè):

(1)已知甲企業(yè)的500件零件質(zhì)量指標值的樣本方差![]() ,該企業(yè)生產(chǎn)的零件質(zhì)量指標值
,該企業(yè)生產(chǎn)的零件質(zhì)量指標值![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,其中
,其中![]() 近似為質(zhì)量指標值的樣本平均數(shù)
近似為質(zhì)量指標值的樣本平均數(shù)![]() (注:求
(注:求![]() 時,同一組數(shù)據(jù)用該區(qū)間的中點值作代表),
時,同一組數(shù)據(jù)用該區(qū)間的中點值作代表),![]() 近似為樣本方差
近似為樣本方差![]() ,試根據(jù)該企業(yè)的抽樣數(shù)據(jù),估計所生產(chǎn)的零件中,質(zhì)量指標值不低于71.92的產(chǎn)品的概率.(精確到0.001)
,試根據(jù)該企業(yè)的抽樣數(shù)據(jù),估計所生產(chǎn)的零件中,質(zhì)量指標值不低于71.92的產(chǎn)品的概率.(精確到0.001)
(2)由以上統(tǒng)計數(shù)據(jù)完成下面![]() 列聯(lián)表,并問能否在犯錯誤的概率不超過0.01的前提下,認為“兩個分廠生產(chǎn)的零件的質(zhì)量有差異”.
列聯(lián)表,并問能否在犯錯誤的概率不超過0.01的前提下,認為“兩個分廠生產(chǎn)的零件的質(zhì)量有差異”.

附注:
參考數(shù)據(jù): ![]() ,
,
參考公式: ![]() ,
, ![]() ,
,
![]() .
.
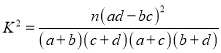
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知以點A(-1,2)為圓心的圓與直線l1:x+2y+7=0相切.過點B(-2,0)的動直線l與圓A相交于M,N兩點,Q是MN的中點.
(1)求圓A的方程;
(2)當|MN|=2![]() 時,求直線l的方程.
時,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】現(xiàn)如今網(wǎng)上購物已經(jīng)習以為常,變成人們?nèi)粘I畹囊徊糠郑瑳_擊著人們的傳統(tǒng)消費習慣、思維和生活方式,以其特殊的優(yōu)勢而逐漸深入人心.某市場調(diào)研機構(gòu)對在“雙十一”購物的![]() 名年齡在
名年齡在![]() 歲的消費者進行了年齡段和性別分布的調(diào)查,其部分結(jié)果統(tǒng)計如下表:
歲的消費者進行了年齡段和性別分布的調(diào)查,其部分結(jié)果統(tǒng)計如下表:
年齡(歲) |
|
|
|
|
|
女 | 70 | 50 | 40 | 30 | 20 |
男 | 30 |
| 20 | 15 | 10 |
(1)若按年齡用分層抽樣的方法抽取84個人,其中在![]() 內(nèi)抽取了36人,求
內(nèi)抽取了36人,求![]() 的值.
的值.
(2)在(1)的條件下,用分層抽樣的方法在![]() 歲的消費者中抽取一個容量為8的本,將該樣本看成一個總體,從中任取3人,記
歲的消費者中抽取一個容量為8的本,將該樣本看成一個總體,從中任取3人,記![]() 表示抽得女性消費者的人數(shù),求隨機變量
表示抽得女性消費者的人數(shù),求隨機變量![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
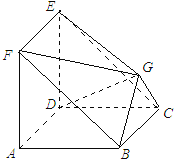
【題目】如圖所示,在多面體![]() 中,四邊形
中,四邊形![]() 與四邊形
與四邊形![]() 均為邊長為2的正方形,
均為邊長為2的正方形,![]() 為等腰直角三角形,
為等腰直角三角形,![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求多面體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
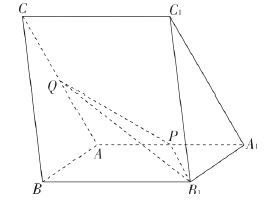
【題目】如圖,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分別為棱
分別為棱![]() 的中點.
的中點.
(1)在平面![]() 內(nèi)過點
內(nèi)過點![]() 作
作![]() 平面
平面![]() 交
交![]() 于點
于點![]() ,并寫出作圖步驟,但不要求證明.
,并寫出作圖步驟,但不要求證明.
(2)若側(cè)面![]() 側(cè)面
側(cè)面![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某電子公司開發(fā)一種智能手機的配件,每個配件的成本是15元,銷售價是20元,月平均銷售![]() 件,通過改進工藝,每個配件的成本不變,質(zhì)量和技術(shù)含金量提高,市場分析的結(jié)果表明,如果每個配件的銷售價提高的百分率為
件,通過改進工藝,每個配件的成本不變,質(zhì)量和技術(shù)含金量提高,市場分析的結(jié)果表明,如果每個配件的銷售價提高的百分率為![]() ,那么月平均銷售量減少的百分率為
,那么月平均銷售量減少的百分率為![]() ,記改進工藝后電子公司銷售該配件的月平均利潤是
,記改進工藝后電子公司銷售該配件的月平均利潤是![]() (元).
(元).
(1)寫出![]() 與
與![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)改進工藝后,試確定該智能手機配件的售價,使電子公司銷售該配件的月平均利潤最大.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若無窮數(shù)列![]() 滿足:
滿足:![]() 恒等于常數(shù)
恒等于常數(shù)![]() ,則稱
,則稱![]() 具有局部等差數(shù)列
具有局部等差數(shù)列![]() .
.
(1)若![]() 具有局部等差數(shù)列
具有局部等差數(shù)列![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若無窮數(shù)列![]() 是等差數(shù)列,無窮數(shù)列
是等差數(shù)列,無窮數(shù)列![]() 是公比為正數(shù)的等比數(shù)列,
是公比為正數(shù)的等比數(shù)列,![]() ,
,![]() ,
,![]() ,判斷
,判斷![]() 是否具有局部等差數(shù)列
是否具有局部等差數(shù)列![]() ,并說明理由;
,并說明理由;
(3)設(shè)![]() 既具有局部等差數(shù)列
既具有局部等差數(shù)列![]() ,又具有局部等差數(shù)列
,又具有局部等差數(shù)列![]() ,求證:
,求證:![]() 具有局部等差數(shù)列
具有局部等差數(shù)列![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com