【題目】是否存在a，b，c使等式（ 
）2+（ 
）2+（ 
）2+…+（ 
）2= 
對一切n∈N*都成立若不存在，說明理由；若存在，用數學歸納法證明你的結論．
【答案】解：取n=1，2，3可得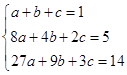 
解得：a= 
，b= 
，c= 
． 下面用數學歸納法證明（ 
）2+（ 
）2+（ 
）2+…+（ 
）2= 
= 
．
即證12+22+…+n2= n（n+1）（2n+1），
①n=1時，左邊=1，右邊=1，∴等式成立；
②假設n=k時等式成立，即12+22+…+k2= k（k+1）（2k+1）成立，
則當n=k+1時，等式左邊=12+22+…+k2+（k+1）2═ k（k+1）（2k+1）+（k+1）2= [k（k+1）（2k+1）+6（k+1）2]= （k+1）（2k2+7k+6）= （k+1）（k+2）（2k+3），
∴當n=k+1時等式成立；
由數學歸納法，綜合①②當n∈N*等式成立，
故存在a= ，b= ，c= 使已知等式成立
【解析】分別取n=1，2，3，得到關于a，b，c的方程組解得即可，先根據當n=1時，把n=1代入求值等式成立；再假設n=k時關系成立，利用變形可得n=k+1時關系也成立，綜合得到對于任意n∈N*時都成立
【考點精析】認真審題，首先需要了解數學歸納法的定義(數學歸納法是證明關于正整數n的命題的一種方法)．
一線名師提優試卷系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）是定義在R上的奇函數，f（x+2）=f（x），當x∈（0，1]時，f（x）=1﹣2|x﹣ 
|，則函數g（x）=f[f（x）]﹣ 
x在區間[﹣2，2]內不同的零點個數是（ ）
A.5
B.6
C.7
D.9
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下表是某廠的產量x與成本y的一組數據：
產量x（千件） | 2 | 3 | 5 | 6 |
成本y（萬元） | 7 | 8 | 9 | 12 |
（Ⅰ）根據表中數據，求出回歸直線的方程 
= 
x 
（其中 = 
， 
= 
﹣ 
）
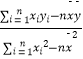（Ⅱ）預計產量為8千件時的成本．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【選修4—4：坐標系與參數方程】
將圓
上每一點的橫坐標保持不變，縱坐標變為原來的2倍，得曲線C.
（Ⅰ）寫出C的參數方程；
（Ⅱ）設直線
與C的交點為
，以坐標原點為極點，x軸正半軸為極軸建立極坐標系，求過線段
的中點且與
垂直的直線的極坐標方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ex ， g（x）=ln 
的圖象分別與直線y=m交于A，B兩點，則|AB|的最小值為（ ）
A.2
B.2+ln2
C.e2 
D.2e﹣ln 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，滿足x2+y2≤1，x≥0，y≥0的點P（x，y）的集合對應的平面圖形的面積為 
；類似的，在空間直角坐標系O﹣xyz中，滿足x2+y2+z2≤1，x≥0，y≥0，z≥0的點P（x，y，z）的集合對應的空間幾何體的體積為（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
