
設(shè)橢圓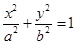 (a>b>0)的兩焦點(diǎn)為F1、F2,若橢圓上存在一點(diǎn)Q,使∠F1QF2=120º,橢圓離心率e的取值范圍為( )
(a>b>0)的兩焦點(diǎn)為F1、F2,若橢圓上存在一點(diǎn)Q,使∠F1QF2=120º,橢圓離心率e的取值范圍為( )
A.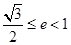 B.
B.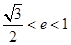 C.
C.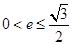 D.
D.
A
【解析】
試題分析:設(shè)Q(x1,y1),F(xiàn)1(-c,0),F(xiàn)2(c,0),c>0,則|QF1|=a+ex1,|QF2|=a-ex1.在△QF1F2中,由余弦定理得 cos120°=-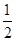 =
= ,解得 x12=
,解得 x12=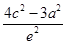 .∵x12∈(0,a2],∴0≤
.∵x12∈(0,a2],∴0≤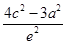 <a2,即4c2-3a2≥0.且e2<1,∴e=
<a2,即4c2-3a2≥0.且e2<1,∴e= ≥
≥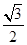 .故橢圓離心率的取范圍是 e∈[
.故橢圓離心率的取范圍是 e∈[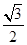 , 1).故選A
, 1).故選A
考點(diǎn):本題考查了橢圓的應(yīng)用
點(diǎn)評:當(dāng)Q點(diǎn)在短軸的端點(diǎn)時∠F1QF2值最大,這個結(jié)論可以記住它.在做選擇題和填空題的時候直接拿來解決這一類的問題


 超能學(xué)典單元期中期末專題沖刺100分系列答案
超能學(xué)典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯(lián)盟沖刺卷系列答案
名校聯(lián)盟沖刺卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年人教版高考數(shù)學(xué)文科二輪專題復(fù)習(xí)提分訓(xùn)練22練習(xí)卷(解析版) 題型:解答題
設(shè)橢圓 +
+ =1(a>b>0)的左,右焦點(diǎn)分別為F1,F2,點(diǎn)P(a,b)滿足|PF2|=|F1F2|.
=1(a>b>0)的左,右焦點(diǎn)分別為F1,F2,點(diǎn)P(a,b)滿足|PF2|=|F1F2|.
(1)求橢圓的離心率e;
(2)設(shè)直線PF2與橢圓相交于A,B兩點(diǎn).若直線PF2與圓(x+1)2+(y- )2=16相交于M,N兩點(diǎn),且|MN|=
)2=16相交于M,N兩點(diǎn),且|MN|= |AB|,求橢圓的方程.
|AB|,求橢圓的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年人教版高考數(shù)學(xué)文科二輪專題復(fù)習(xí)提分訓(xùn)練22練習(xí)卷(解析版) 題型:解答題
設(shè)橢圓 +
+ =1(a>b>0)的左焦點(diǎn)為F,離心率為
=1(a>b>0)的左焦點(diǎn)為F,離心率為 ,過點(diǎn)F且與x軸垂直的直線被橢圓截得的線段長為
,過點(diǎn)F且與x軸垂直的直線被橢圓截得的線段長為 .
.
(1)求橢圓的方程;
(2)設(shè)A,B分別為橢圓的左、右頂點(diǎn),過點(diǎn)F且斜率為k的直線與橢圓交于C,D兩點(diǎn).若 ·
· +
+ ·
· =8,求k的值.
=8,求k的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年四川省高三高考極限壓軸文科數(shù)學(xué)試卷(解析版) 題型:解答題
設(shè)橢圓C: (“a>b〉0)的左焦點(diǎn)為
(“a>b〉0)的左焦點(diǎn)為 ,橢圓過點(diǎn)P(
,橢圓過點(diǎn)P( )
)
(1)求橢圓C的方程;
(2)已知點(diǎn)D(1, 0),直線l: 與橢圓C交于A、B兩點(diǎn),以DA和DB為鄰邊的四邊形是菱形,求k的取值范圍.
與橢圓C交于A、B兩點(diǎn),以DA和DB為鄰邊的四邊形是菱形,求k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:期中題 題型:解答題
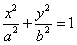 (a>b>0)的左焦點(diǎn)為F1(-2,0),左準(zhǔn)線
(a>b>0)的左焦點(diǎn)為F1(-2,0),左準(zhǔn)線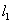 與x軸交于點(diǎn)N(-3,0),過點(diǎn)N傾斜角為30°的直線
與x軸交于點(diǎn)N(-3,0),過點(diǎn)N傾斜角為30°的直線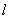 交橢圓于A,B兩點(diǎn)。
交橢圓于A,B兩點(diǎn)。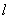 和橢圓的方程;
和橢圓的方程;查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com