
【題目】已知函數![]()
(1)若函數![]() 在
在![]() 處取得極值1,證明:
處取得極值1,證明:![]()
(2)若![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)證明見詳解;(2)![]()
【解析】
(1)求出函數![]() 的導函數
的導函數![]() ,由
,由![]() 在
在![]() 處取得極值1,可得
處取得極值1,可得![]() 且
且![]() .解出
.解出![]() ,構造函數
,構造函數![]() ,分析其單調性,結合
,分析其單調性,結合![]() ,即可得到
,即可得到![]() 的范圍,命題得證;
的范圍,命題得證;
(2)由![]() 分離參數,得到
分離參數,得到![]() 恒成立,構造函數
恒成立,構造函數![]() ,求導函數
,求導函數![]() ,再構造函數
,再構造函數![]() ,進行二次求導
,進行二次求導![]() .由
.由![]() 知
知![]() ,則
,則![]() 在
在![]() 上單調遞增.根據零點存在定理可知
上單調遞增.根據零點存在定理可知![]() 有唯一零點
有唯一零點![]() ,且
,且![]() .由此判斷出
.由此判斷出![]() 時,
時,![]() 單調遞減,
單調遞減,![]() 時,
時,![]() 單調遞增,則
單調遞增,則![]() ,即
,即![]() .由
.由![]() 得
得![]() ,再次構造函數
,再次構造函數![]() ,求導分析單調性,從而得
,求導分析單調性,從而得![]() ,即
,即![]() ,最終求得
,最終求得![]() ,則
,則![]() .
.
解:(1)由題知,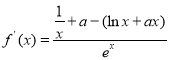
∵函數![]() 在
在![]() ,處取得極值1,
,處取得極值1,
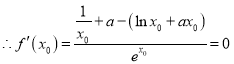 ,且
,且![]() ,
,
![]() ,
,
![]() ,
,
令![]() ,則
,則![]()
![]() 為增函數,
為增函數,
![]()
![]() ,即
,即![]() 成立.
成立.
(2)不等式![]() 恒成立,
恒成立,
即不等式![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
令![]() ,則
,則![]()
令![]() ,則
,則![]() ,
,
![]() ,
,![]() ,
,
![]() 在
在![]() 上單調遞增,且
上單調遞增,且![]() ,
,
![]() 有唯一零點
有唯一零點![]() ,且
,且![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,
,![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,
,![]() ,
,![]() 單調遞增.
單調遞增.
![]() ,
,
![]()
由![]() 整理得
整理得![]()
![]() ,
,![]()
令![]() ,則方程
,則方程![]() 等價于
等價于![]()
而![]() 在
在![]() 上恒大于零,
上恒大于零,
![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() .
.
![]()
![]()
![]() ,
,
![]()
∴實數![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
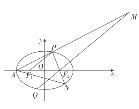
【題目】已知橢圓![]() 的左頂點為
的左頂點為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,離心率為
,離心率為![]() ,
,![]() 是橢圓上的一個動點(不與左、右頂點重合),且
是橢圓上的一個動點(不與左、右頂點重合),且![]() 的周長為6,點
的周長為6,點![]() 關于原點的對稱點為
關于原點的對稱點為![]() ,直線
,直線![]() 交于點
交于點![]() .
.
(1)求橢圓方程;
(2)若直線![]() 與橢圓交于另一點
與橢圓交于另一點![]() ,且
,且![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《易經》是中國傳統文化中的精髓,如圖是易經八卦(含乾、坤、巽、震、坎、離、艮、兌八卦),每一卦由三根線組成("![]() "表示一根陽線,"
"表示一根陽線,"![]() "表示一根陰線),從八卦中任取兩卦,這兩卦的六根線中恰有兩根陽線,四根陰線的概率為_______.
"表示一根陰線),從八卦中任取兩卦,這兩卦的六根線中恰有兩根陽線,四根陰線的概率為_______.

查看答案和解析>>
科目:高中數學 來源: 題型:
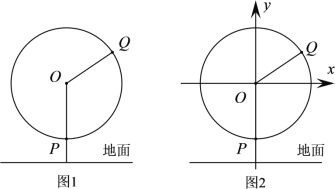
【題目】隨著我國綜合國力的不斷增強,不少綜合性娛樂場所都引進了“摩天輪”這一娛樂設施.(如圖1)有一半徑為40m的摩天輪,軸心![]() 距地面50m,摩天輪按逆時針方向做勻速旋轉,轉一周需要3min.點
距地面50m,摩天輪按逆時針方向做勻速旋轉,轉一周需要3min.點![]() 與點
與點![]() 都在摩天輪上,且點
都在摩天輪上,且點![]() 相對于點
相對于點![]() 落后1min,當點
落后1min,當點![]() 在摩天輪的最低點處時開始計時,以軸心
在摩天輪的最低點處時開始計時,以軸心![]() 為坐標原點,平行于地面且在摩天輪所在平面內的直線為
為坐標原點,平行于地面且在摩天輪所在平面內的直線為![]() 軸,建立圖2所示的平面直角坐標系.
軸,建立圖2所示的平面直角坐標系.

(1)若![]() ,求點
,求點![]() 的縱坐標關于時間
的縱坐標關于時間![]() 的函數關系式
的函數關系式![]() ;
;
(2)若![]() ,求點
,求點![]() 距離地面的高度關于時間
距離地面的高度關于時間![]() 的函數關系式
的函數關系式![]() ,并求
,并求![]() 時,點
時,點![]() 離地面的高度(結果精確到0.1,計算所用數據:
離地面的高度(結果精確到0.1,計算所用數據:![]() )
)
(3)若![]() ,當
,當![]() ,
,![]() 兩點距離地面的高度差不超過
兩點距離地面的高度差不超過![]() 時,求時間
時,求時間![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com