
【題目】2020年4月8日,武漢市雷神山醫院為確診新型冠狀病毒肺炎患者,需要檢測核酸是否為陽性,現有![]() 份核酸樣本,有以下兩種檢測方式:(1)逐份檢測,則需要檢測
份核酸樣本,有以下兩種檢測方式:(1)逐份檢測,則需要檢測![]() 次;(2)混合檢測,將其中
次;(2)混合檢測,將其中![]() (
(![]() ,且
,且![]() )份核酸樣本分別取樣混合在一起檢測,若檢測結果為陰性,這
)份核酸樣本分別取樣混合在一起檢測,若檢測結果為陰性,這![]() 份核酸樣本全為陰性,因而這
份核酸樣本全為陰性,因而這![]() 份核酸樣本只要檢測一次就夠了,如果檢測結果為陽性,為了明確這
份核酸樣本只要檢測一次就夠了,如果檢測結果為陽性,為了明確這![]() 份核酸樣本究竟哪幾份為陽性,就要對這
份核酸樣本究竟哪幾份為陽性,就要對這![]() 份樣本再逐份檢測,此時這
份樣本再逐份檢測,此時這![]() 份核酸樣本的檢測次數總共為
份核酸樣本的檢測次數總共為![]() 次.假設在接受檢測的核酸樣本中,每份樣本的檢測結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為
次.假設在接受檢測的核酸樣本中,每份樣本的檢測結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為![]() .
.
(1)假設有5份核酸樣本,其中只有2份樣本為陽性,若采用逐份檢測方式,求恰好經過4次檢測就能把陽性樣本全部檢測出來的概率.
(2)現取其中![]() (
(![]() ,且
,且![]() )份核酸樣本,記采用逐份檢測方式,樣本需要檢測的總次數為
)份核酸樣本,記采用逐份檢測方式,樣本需要檢測的總次數為![]() ,采用混合檢測方式,樣本需要檢測的總次數為
,采用混合檢測方式,樣本需要檢測的總次數為![]() .
.
①試運用概率統計的知識,若![]() ,試求
,試求![]() 關于
關于![]() 的函數關系式
的函數關系式![]() ;
;
②若![]() ,用混合檢測方式可以使得樣本需要檢測的總次數的期望值比逐份檢測的總次數期望值更少,求
,用混合檢測方式可以使得樣本需要檢測的總次數的期望值比逐份檢測的總次數期望值更少,求![]() 的最大值.
的最大值.
參考數據:![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】若數列![]() 滿足
滿足![]() ,
,![]() ,記數列
,記數列![]() 的前n項和是
的前n項和是![]() ,則( )
,則( )
A.若數列![]() 是常數列,則
是常數列,則![]()
B.若![]() ,則數列
,則數列![]() 單調遞減
單調遞減
C.若![]() ,則
,則![]()
D.若![]() ,任取
,任取![]() 中的9項
中的9項![]() 構成數列
構成數列![]() 的子數列
的子數列![]() ,則
,則![]() 不全是單調數列
不全是單調數列
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年新型冠狀病毒肺炎(簡稱“新冠肺炎”)成為威脅全球的公共衛生問題,中醫藥在本次新冠肺炎的治療中發揮了重要作用.研究人員對66例普通型新冠肺炎恢復期患者進行了中醫臨床特征分析,發現主要證型有氣陰兩虛證與肺脾氣虛證,同時可能兼夾濕證.為研究這兩種主要證型在兼夾濕證的難易上是否有差異,研究人員將濕證癥狀分級量化,將所有肺脾氣虛證患者的量化分作成莖葉圖.
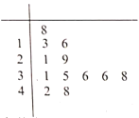
(1)若量化分不低于16分,即可診斷為兼夾濕證,請參考莖葉圖,完成下面![]() 列聯表.
列聯表.
夾濕證 | 非夾濕證 | 合計 | |
氣陰兩虛 | 20 | ||
肺脾氣虛 | |||
合計 | 66 |
(2)根據此資料,能否有99%的把握認為兩種主要證型在兼夾濕證的難易上有差異?
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
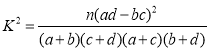
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓P經過點![]() ,并且與圓
,并且與圓![]() 相切.
相切.
(Ⅰ)求圓心P的軌跡C的方程;
(Ⅱ)O是坐標原點,過點![]() 的直線
的直線![]() 與C交于A,B兩點,在C上是否存在點Q,使得四邊形
與C交于A,B兩點,在C上是否存在點Q,使得四邊形![]() 是平行四邊形?
是平行四邊形?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻轉成
翻轉成![]() (
(![]() 平面
平面![]() ).若
).若![]() 分別為線段
分別為線段![]() 的中點,則在
的中點,則在![]() 翻轉過程中,下列說法正確的是( )
翻轉過程中,下列說法正確的是( )
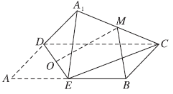
A.與平面![]() 垂直的直線必與直線
垂直的直線必與直線![]() 垂直
垂直
B.異面直線![]() 與
與![]() 所成的角是定值
所成的角是定值
C.一定存在某個位置,使![]()
D.三棱錐![]() 外接球半徑與棱
外接球半徑與棱![]() 的長之比為定值
的長之比為定值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,將直角梯形ABCD(及其內部)以AB所在直線為軸順時針旋轉90°,形成如圖所示的幾何體,其中M為
,將直角梯形ABCD(及其內部)以AB所在直線為軸順時針旋轉90°,形成如圖所示的幾何體,其中M為![]() 的中點.
的中點.
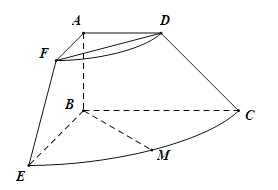
(1)求證:![]() ;
;
(2)求異面直線BM與EF所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=ex+asinx,x∈(-π,+∞),下列說法正確的是( )
A.當a=1時,f(x)在(0,f(0))處的切線方程為2x-y+1=0
B.當a=1時,f(x)存在唯一極小值點x0且-1<f(x0)<0
C.對任意a>0,f(x)在(-π,+∞)上均存在零點
D.存在a<0,f(x)在(-π,+∞)上有且只有一個零點
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com