
【題目】已知動圓P經過點![]() ,并且與圓
,并且與圓![]() 相切.
相切.
(Ⅰ)求圓心P的軌跡C的方程;
(Ⅱ)O是坐標原點,過點![]() 的直線
的直線![]() 與C交于A,B兩點,在C上是否存在點Q,使得四邊形
與C交于A,B兩點,在C上是否存在點Q,使得四邊形![]() 是平行四邊形?
是平行四邊形?
【答案】(1) ![]() ;
;
(2) 直線![]() 為
為![]() 或
或![]() 時,橢圓C上存在點Q,否則不存在.
時,橢圓C上存在點Q,否則不存在.
【解析】
(1) 由橢圓的定義可得,P的軌跡是以M,N為焦點的橢圓,進而求出方程.
(2) 假設存在,根據平行四邊形已知三個點坐標,表示Q的坐標,設直線方程,聯立直線和橢圓方程,利用韋達定理整理Q的坐標,根據Q在橢圓上,求得直線方程.
(1) 由題意可得N在圓M內部,所以兩圓內切,
所以![]() ,
,
由橢圓的定義可知,點![]() 的軌跡是以
的軌跡是以![]() ,
,![]() 為焦點的橢圓,
為焦點的橢圓,
設橢圓方程為![]() ,
,
其中![]() ,
,![]() ,
,
所以![]() ,
,
所以點![]() 的軌跡
的軌跡![]() 的方程為
的方程為![]() .
.
(2) 假設C上存在點Q,使得四邊形![]() 是平行四邊形,
是平行四邊形,
由題意可知,直線![]() 的斜率存在,設直線
的斜率存在,設直線![]() 的方程為:
的方程為:![]()
設直線![]() 與橢圓C的交點
與橢圓C的交點![]() ,
,
則![]()
聯立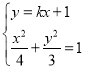 可得,
可得,![]()
由韋達定理可得,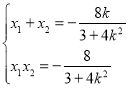
![]()
所以![]() ,
,
點 Q在橢圓C上,所以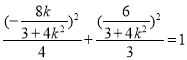 ,
,
解得![]()
綜上可得,直線![]() 為
為![]() 或
或![]() 時,
時,
橢圓C上存在點Q,使得四邊形![]() 是平行四邊形,否則不存在.
是平行四邊形,否則不存在.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為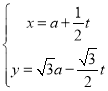 (
(![]() 為參數,
為參數,![]() ).在以坐標原點為極點、
).在以坐標原點為極點、![]() 軸的非負半軸為極軸的極坐標系中,曲線
軸的非負半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若點![]() 在直線
在直線![]() 上,求直線
上,求直線![]() 的極坐標方程;
的極坐標方程;
(2)已知![]() ,若點
,若點![]() 在直線
在直線![]() 上,點
上,點![]() 在曲線
在曲線![]() 上,且
上,且![]() 的最小值為
的最小值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校數學建模小組為了研究雙層玻璃窗戶中每層玻璃厚度![]() (每層玻璃的厚度相同)及兩層玻璃間夾空氣層厚度
(每層玻璃的厚度相同)及兩層玻璃間夾空氣層厚度![]() 對保溫效果的影響,利用熱傳導定律得到熱傳導量
對保溫效果的影響,利用熱傳導定律得到熱傳導量![]() 滿足關系式
滿足關系式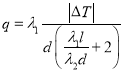 ,其中玻璃的熱傳導系數
,其中玻璃的熱傳導系數![]() 焦耳/(厘米·度),不流通、干燥空氣的熱傳導系數
焦耳/(厘米·度),不流通、干燥空氣的熱傳導系數![]() 焦耳/(厘米·度),
焦耳/(厘米·度),![]() 為室內外溫度差,
為室內外溫度差,![]() 值越小,保溫效果越好,現有4種型號的雙層玻璃窗戶,具體數據如下表:
值越小,保溫效果越好,現有4種型號的雙層玻璃窗戶,具體數據如下表:
型號 | 每層玻璃厚度 | 玻璃間夾空氣層厚度 |
| 0.4 | 3 |
| 0.3 | 4 |
| 0.5 | 3 |
| 0.4 | 4 |
則保溫效果最好的雙層玻璃的型號是( )
A.![]() 型B.
型B.![]() 型C.
型C.![]() 型D.
型D.![]() 型
型
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D與AD1交于點E,AA1=AD=2AB=4.
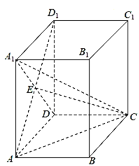
(1)證明:AE⊥平面ECD;
(2)求點C1到平面AEC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四面體![]() 中,棱
中,棱![]() ,
,![]() 所在直線所成角為
所在直線所成角為![]() ,且
,且![]() ,
,![]() ,
,![]() ,面
,面![]() 和面
和面![]() 所成的銳二面角為
所成的銳二面角為![]() ,面
,面![]() 和面
和面![]() 所成的銳二面角為
所成的銳二面角為![]() ,當四面體
,當四面體![]() 的體積取得最大值時( ).
的體積取得最大值時( ).
A.![]() B.
B.![]() C.
C.![]() D.不能確定
D.不能確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的點,
上的點,![]() ,
,![]() 為
為![]() 的中點.將
的中點.將![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得
的位置,使得![]() ,如圖2.
,如圖2.
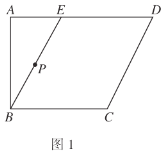
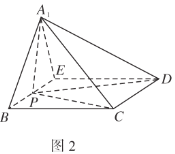
(1)求證:平面![]() 平面
平面![]() ;
;
(2)點![]() 在線段
在線段![]() 上,當直線
上,當直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年4月8日,武漢市雷神山醫院為確診新型冠狀病毒肺炎患者,需要檢測核酸是否為陽性,現有![]() 份核酸樣本,有以下兩種檢測方式:(1)逐份檢測,則需要檢測
份核酸樣本,有以下兩種檢測方式:(1)逐份檢測,則需要檢測![]() 次;(2)混合檢測,將其中
次;(2)混合檢測,將其中![]() (
(![]() ,且
,且![]() )份核酸樣本分別取樣混合在一起檢測,若檢測結果為陰性,這
)份核酸樣本分別取樣混合在一起檢測,若檢測結果為陰性,這![]() 份核酸樣本全為陰性,因而這
份核酸樣本全為陰性,因而這![]() 份核酸樣本只要檢測一次就夠了,如果檢測結果為陽性,為了明確這
份核酸樣本只要檢測一次就夠了,如果檢測結果為陽性,為了明確這![]() 份核酸樣本究竟哪幾份為陽性,就要對這
份核酸樣本究竟哪幾份為陽性,就要對這![]() 份樣本再逐份檢測,此時這
份樣本再逐份檢測,此時這![]() 份核酸樣本的檢測次數總共為
份核酸樣本的檢測次數總共為![]() 次.假設在接受檢測的核酸樣本中,每份樣本的檢測結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為
次.假設在接受檢測的核酸樣本中,每份樣本的檢測結果是陽性還是陰性都是獨立的,且每份樣本是陽性結果的概率為![]() .
.
(1)假設有5份核酸樣本,其中只有2份樣本為陽性,若采用逐份檢測方式,求恰好經過4次檢測就能把陽性樣本全部檢測出來的概率.
(2)現取其中![]() (
(![]() ,且
,且![]() )份核酸樣本,記采用逐份檢測方式,樣本需要檢測的總次數為
)份核酸樣本,記采用逐份檢測方式,樣本需要檢測的總次數為![]() ,采用混合檢測方式,樣本需要檢測的總次數為
,采用混合檢測方式,樣本需要檢測的總次數為![]() .
.
①試運用概率統計的知識,若![]() ,試求
,試求![]() 關于
關于![]() 的函數關系式
的函數關系式![]() ;
;
②若![]() ,用混合檢測方式可以使得樣本需要檢測的總次數的期望值比逐份檢測的總次數期望值更少,求
,用混合檢測方式可以使得樣本需要檢測的總次數的期望值比逐份檢測的總次數期望值更少,求![]() 的最大值.
的最大值.
參考數據:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從![]() 年底開始,非洲東部的肯尼亞等國家爆發出了一場嚴重的蝗蟲災情.目前,蝗蟲已抵達烏干達和坦桑尼亞,并向西亞和南亞等地區蔓延.蝗蟲危害大,主要危害禾本科植物,能對農作物造成嚴重傷害,每只蝗蟲的平均產卵數
年底開始,非洲東部的肯尼亞等國家爆發出了一場嚴重的蝗蟲災情.目前,蝗蟲已抵達烏干達和坦桑尼亞,并向西亞和南亞等地區蔓延.蝗蟲危害大,主要危害禾本科植物,能對農作物造成嚴重傷害,每只蝗蟲的平均產卵數![]() 和平均溫度
和平均溫度![]() 有關,現收集了以往某地的
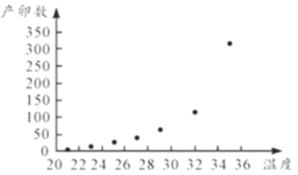
有關,現收集了以往某地的![]() 組數據,得到下面的散點圖及一些統計量的值.
組數據,得到下面的散點圖及一些統計量的值.
平均溫度 |
|
|
|
|
|
|
|
平均產卵數 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
(1)根據散點圖判斷,![]() 與
與![]() (其中
(其中![]() 為自然對數的底數)哪一個更適宜作為平均產卵數
為自然對數的底數)哪一個更適宜作為平均產卵數![]() 關于平均溫度
關于平均溫度![]() 的回歸方程類型?(給出判斷即可,不必說明理由)并由判斷結果及表中數據,求出
的回歸方程類型?(給出判斷即可,不必說明理由)并由判斷結果及表中數據,求出![]() 關于
關于![]() 的回歸方程.(結果精確到小數點后第三位)
的回歸方程.(結果精確到小數點后第三位)
(2)根據以往統計,該地每年平均溫度達到![]() 以上時蝗蟲會造成嚴重傷害,需要人工防治,其他情況均不需要人工防治,記該地每年平均溫度達到
以上時蝗蟲會造成嚴重傷害,需要人工防治,其他情況均不需要人工防治,記該地每年平均溫度達到![]() 以上的概率為
以上的概率為![]() .
.
①記該地今后![]() 年中,恰好需要
年中,恰好需要![]() 次人工防治的概率為
次人工防治的概率為![]() ,求
,求![]() 取得最大值時相應的概率
取得最大值時相應的概率![]() ;
;
②根據①中的結論,當![]() 取最大值時,記該地今后
取最大值時,記該地今后![]() 年中,需要人工防治的次數為
年中,需要人工防治的次數為![]() ,求
,求![]() 的數學期望和方差.
的數學期望和方差.
附:對于一組數據![]() 、
、![]() 、
、![]() 、
、![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘法估計分別為:
的斜率和截距的最小二乘法估計分別為: ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代十進制的算籌計數法,在數學史上是一個偉大的創造,算籌實際上是一根根同長短的小木棍.如圖,是利用算籌表示數1-9的一種方法.例如:3可表示為“≡”,26可表示為“=⊥”,現有6根算籌,據此表示方法,若算籌不能剩余,則可以用1-9這9個數字表示兩位數中,能被3整除的概率是( )
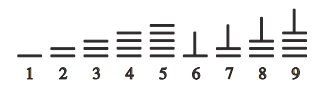
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com