
【題目】對于定義域為![]() 的函數
的函數![]() ,若同時滿足下列條件:
,若同時滿足下列條件:
①![]() 在
在![]() 內單調遞增或單調遞減;
內單調遞增或單調遞減;
②存在區間![]() ,使
,使![]() 在
在![]() 上的值域為
上的值域為![]() ;那么把
;那么把![]() (
(![]() )叫閉函數.
)叫閉函數.
(1)求閉函數![]() 符合條件②的區間
符合條件②的區間![]() ;
;
(2)判斷函數![]() 是否為閉函數?并說明理由;
是否為閉函數?并說明理由;
(3)判斷函數![]() 是否為閉函數?若是閉函數,求實數
是否為閉函數?若是閉函數,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)不是閉函數,理由見解析;(3)
;(2)不是閉函數,理由見解析;(3)![]() .
.
【解析】
試題分析:(1)根據閉函數的定義解![]() 即可;(2)先判斷函數的單調性,再根據閉函數的定義判斷;(3)先假設函數為閉函數,從而得到
即可;(2)先判斷函數的單調性,再根據閉函數的定義判斷;(3)先假設函數為閉函數,從而得到![]() 為方程
為方程![]() 的兩個實根,從而利用韋達定理與二次函數的圖象與性質求得實數
的兩個實根,從而利用韋達定理與二次函數的圖象與性質求得實數![]() 的取值范圍.
的取值范圍.
試題解析:(1)由題意,![]() 在
在![]() 上遞減,則
上遞減,則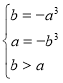 ,解得
,解得![]() ,
,
所以,所求的區間為![]() .
.
(2)取![]() ,則
,則![]() ,即
,即![]() 不是
不是![]() 上的減函數,
上的減函數,
取![]() ,即
,即![]() 不是
不是![]() 上的增函數,
上的增函數,
所以函數在定義域內不單調遞增或單調遞減,從而該函數不是閉函數.
(3)若![]() 是閉函數,則存在區間
是閉函數,則存在區間![]() ,在區間
,在區間![]() 上,函數
上,函數![]() 的值域為
的值域為![]() ,
,
即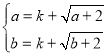 ,∴
,∴![]() 為方程
為方程![]() 的兩個實根,
的兩個實根,
即方程![]() 有兩個不等的實根,
有兩個不等的實根,
當![]() 時,有
時,有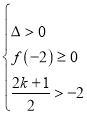 ,解得
,解得![]() ,當
,當![]() 時,有
時,有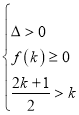 ,無解.
,無解.
綜上所述,![]() .
.


 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯盟沖刺卷系列答案
名校聯盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中數學 來源: 題型:
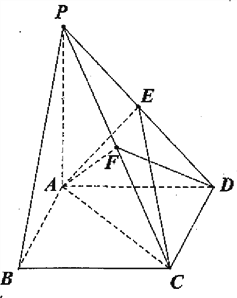
【題目】如圖,四棱錐P—ABCD的底面ABCD為矩形,PA⊥平面ABCD,點E是棱PD的中點,點F是PC的中點.
(Ⅰ)證明:PB∥平面AEC;
(Ⅱ)若底面ABCD為正方形,![]() ,求二面角C—AF—D大小.
,求二面角C—AF—D大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某租賃公司擁有汽車100輛,當每輛車的月租金為3000元時,可全部租出.若每輛車的月租金每增加50元,未租出的車將會增加一輛,租出的車每輛每月需要維護費150元,未租出的車每輛每月需要維護費50元.
(1)當每輛車的月租金定為3600元時,能租出多少輛車?
(2)當每輛車的月租金定為多少元時,租賃公司的月收益最大,最大月收益是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產某種產品時的能耗y與產品件數x之間的關系式為y=ax+![]() .且當x=2時,y=100;當x=7時,y=35.且此產品生產件數不超過20件.
.且當x=2時,y=100;當x=7時,y=35.且此產品生產件數不超過20件.
(1)寫出函數y關于x的解析式;
(2)用列表法表示此函數,并畫出圖象.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() .
.
(1)求f(2)+f![]() ,f(3)+f
,f(3)+f![]() 的值;
的值;
(2)求證:f(x)+f![]() 是定值;
是定值;
(3)求f(2)+f![]() +f(3)+f
+f(3)+f![]() +…+
+…+![]() +f
+f![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了對2016年某校中考成績進行分析,在60分以上的全體同學中隨機抽出8位,他們的數學分數(已折算為百分制)從小到大排是60、65、70、75、80、85、90、95,物理分數從小到大排是72、77、80、84、88、90、93、95.
(1)若規定85分(包括85分)以上為優秀,求這8位同學中恰有3位同學的數學和物理分數均為優秀的概率;
(2)若這8位同學的數學、物理、化學分數事實上對應如下表:
學生編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
數學分數 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分數 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
化學分數 | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
①用變量![]() 與
與![]() 與
與![]() 的相關系數說明物理與數學、化學與數學的相關程度;
的相關系數說明物理與數學、化學與數學的相關程度;
②求![]() 與
與![]() 與
與![]() 的線性回歸方程(系數精確到0.01),當某同學的數學成績為50分時,估計其物理、化學兩科的得分.
的線性回歸方程(系數精確到0.01),當某同學的數學成績為50分時,估計其物理、化學兩科的得分.
參考公式:相關系數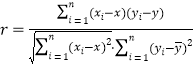 ,
,
回歸直線方程是:![]() ,其中
,其中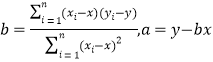 ,
,
參考數據: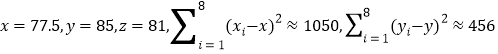 ,
,![]() ,
,![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車站每天均有3輛開往省城的分為上、中、下等級的客車,某天袁先生準備在該汽車站乘車前往省城辦事,但他不知道客車的車況,也不知道發車順序.為了盡可能乘上上等車,他采取如下策略:先放過一輛,如果第二輛比第一輛好則上第二輛,否則上第三輛.則他乘上上等車的概率為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com