
【題目】在![]() 中,內角
中,內角![]() 的對邊分別為
的對邊分別為![]() ,已知
,已知![]() .
.
(Ⅰ)求角![]() 的值;
的值;
(Ⅱ)若![]() ,當
,當![]() 取最小值時,求
取最小值時,求![]() 的面積.
的面積.
【答案】(1)![]() (2)
(2)![]()
【解析】
試題分析:方法一:(Ⅰ)利用正弦定理、誘導公式、兩角和的正弦公式化簡已知的式子,由內角的范圍和特殊角的三角函數值求出角C;(Ⅱ)利用余弦定理列出方程,由條件和完全平方公式化簡后,利用基本不等式求出c的最小值,由面積公式求出△ABC的面積;方法二:(Ⅰ)利用余弦定理化簡已知的式子得到邊的關系,由余弦定理求出cosC的值,由內角的范圍和特殊角的三角函數值求出角C;(Ⅱ)利用余弦定理列出方程,結合條件消元后,利用一元二次函數的性質求出c的最小值,由面積公式求出△ABC的面積
試題解析:解法一(1)∵![]() ,∴
,∴![]() ……………………1分
……………………1分
∴![]() ……………2分
……………2分
即 ![]() ……………3分
……………3分
∴![]() 4分
4分
∵![]() ∴
∴ ![]() …………5分
…………5分
又∵![]() 是三角形的內角,∴
是三角形的內角,∴![]() ……6分
……6分
(2)由余弦定理得:![]() …………7分
…………7分
∵ ![]() ,故
,故![]() 8分
8分
∴ ![]() (當且僅當
(當且僅當![]() 時等號成立) ………10分
時等號成立) ………10分
∴![]() 的最小值為2,故
的最小值為2,故![]() ……12分
……12分
解法二:(1)∵![]() ,∴
,∴ ![]() ………1分
………1分
∴ ![]() ,即
,即 ![]() …………3分
…………3分
∴ ![]() …5分
…5分
又∵![]() 是三角形的內角,∴
是三角形的內角,∴![]() 6分
6分
(2)由已知,![]() ,即
,即![]() ,故:
,故:
![]() ……………8分
……………8分
∴ ![]() …………10分
…………10分
∴當![]() 時,
時,![]() 的最小值為2,故
的最小值為2,故![]() …………12分
…………12分


 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:高中數學 來源: 題型:
【題目】已知三次函數![]() ,下列命題正確的是 .
,下列命題正確的是 .
①函數![]() 關于原點
關于原點![]() 中心對稱;
中心對稱;
②以![]() ,
,![]() 兩不同的點為切點作兩條互相平行的切線,分別與
兩不同的點為切點作兩條互相平行的切線,分別與![]() 交于
交于![]() 兩點,則這四個點的橫坐標滿足關系
兩點,則這四個點的橫坐標滿足關系![]() ;
;
③以![]() 為切點,作切線與
為切點,作切線與![]() 圖像交于點
圖像交于點![]() ,再以點
,再以點![]() 為切點作直線與
為切點作直線與![]() 圖像交于點
圖像交于點![]() ,再以點
,再以點![]() 作切點作直線與
作切點作直線與![]() 圖像交于點
圖像交于點![]() ,則
,則![]() 點橫坐標為
點橫坐標為![]() ;
;
④若![]() ,函數
,函數![]() 圖像上存在四點
圖像上存在四點![]() ,使得以它們為頂點的四邊形有且僅有一個正方形.
,使得以它們為頂點的四邊形有且僅有一個正方形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產甲乙兩種產品均需用A,B兩種原料,已知生產1噸每種產品需原料及每天原料的可用限額如右表所示,如果生產1噸甲、乙產品可獲利潤分別為3萬元、4萬元,則該企業每天可獲得最大利潤為( )
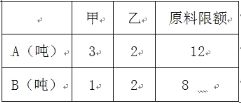
A.12萬元 B.16萬元
C.17萬元 D.18萬元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知方程![]() .
.
(1)求該方程表示一條直線的條件;
(2)當![]() 為何實數時,方程表示的直線斜率不存在?求出這時的直線方程;
為何實數時,方程表示的直線斜率不存在?求出這時的直線方程;
(3)已知方程表示的直線![]() 在
在![]() 軸上的截距為-3,求實數
軸上的截距為-3,求實數![]() 的值;
的值;
(4)若方程表示的直線![]() 的傾斜角是45°,求實數
的傾斜角是45°,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() .
.
(1)在區間![]() 上畫出函數
上畫出函數![]() 的圖象;
的圖象;
(2)設集合![]() ,
,![]() .試判斷集合
.試判斷集合![]() 和
和![]() 之間的關系,并給出證明;
之間的關系,并給出證明;
(3)當![]() 時,求證:在區間
時,求證:在區間![]() 上,
上,![]() 的圖象位于函數
的圖象位于函數![]() 圖象的上方.
圖象的上方.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班一次數學考試成績頻率分布直方圖如圖所示,數據分組依次為![]() ,已知成績大于等于
,已知成績大于等于![]() 分的人數為
分的人數為![]() 人,現采用分層抽樣的方式抽取一個容量為
人,現采用分層抽樣的方式抽取一個容量為![]() 的樣本.
的樣本.
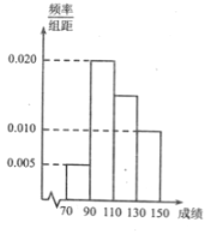
(1)求每個分組所抽取的學生人數;
(2)從數學成績在![]() 的樣本中任取
的樣本中任取![]() 人,求恰有
人,求恰有![]() 人成績在
人成績在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司今年年初用25萬元引進一種新的設備,投入設備后每年收益為21萬元。該公司第n年需要付出設備的維修和工人工資等費用![]() 的信息如下圖。
的信息如下圖。
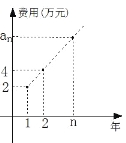
(Ⅰ)求![]() ;
;
(Ⅱ)引進這種設備后,第幾年后該公司開始獲利;
(Ⅲ)這種設備使用多少年,該公司的年平均獲利最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com