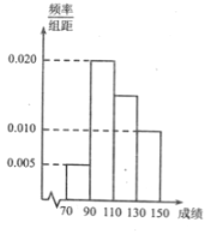
【題目】某班一次數學考試成績頻率分布直方圖如圖所示，數據分組依次為
，已知成績大于等于
分的人數為
人，現采用分層抽樣的方式抽取一個容量為
的樣本.
（1）求每個分組所抽取的學生人數；
（2）從數學成績在
的樣本中任取
人，求恰有
人成績在
的概率.
【答案】（1）
；（2）
.
【解析】
試題分析：（1）數學成績在
內的頻率分別為
.比為
，所以采用分層抽樣的方式抽取一個容量為
的樣本，人數分別為；（2）由（1）可知，從
兩組抽取人數分別為
人和
人，利用列舉法求得總事件有
種，其中符合題意的有
種，故概率為.
試題解析：
（1）由頻率分布直方圖可知，
數學成績在內的頻率分別為.
∴成績在
內的人數之比為，
∴采用分層抽樣的方式抽取一個容量為的樣本，成績在內所抽取的人數分別為.
（2）由（1）可知，從兩組抽取人數分別為人和人，
記從
中抽取的
人分別為
，從
中抽取的
人分別為
，從這
個人中任取人，有
，
共計種等可能的結果，其中恰有
人成績在
包含
，共計
種等可能的結果，
∴抽取的人中恰有
人成績在的概率
.
中考解讀考點精練系列答案科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，
，動點
滿足
（
且
）.
（1）求動點
的軌跡方程，并說明軌跡是什么曲線；
（2）若
，點
為動點
的軌跡曲線上的任意一點，過點
作圓：
的切線，切點為
.試探究平面內是否存在定點
，使
為定值，若存在，請求出點
的坐標，若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，PA垂直于矩形ABCD所在的平面，E、F分別是AB、PD的中點，∠ADP＝45°.
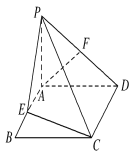
（1）求證：AF∥平面PCE.
（2）求證：平面PCD⊥平面PCE.
（3）若AD＝2，CD＝3，求點F到平面PCE的距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知四棱錐P－ABCD的底面是邊長為1的正方形，且側棱PC⊥底面ABCD，且PC＝2，E是側棱PC上的動點
（1）求四棱錐P－ABCD的體積；
（2）證明：BD⊥AE。
（3）求二面角P-BD-C的正切值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，已知橢圓
：
的離心率
，左頂點為
，過點
作斜率為
的直線
交橢圓于點
，交
軸于點
.
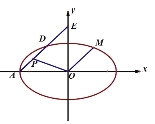
（1）求橢圓的方程;
（2）已知
為
的中點，存在定點
，使得對于任意的都有
，求點的坐標;
（3）若過
點作直線
的平行線交橢圓于點
，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某車間甲組有10名工人，其中有4名女工人；乙組有10名工人，其中有6名女工人．現采用分層抽樣方法（層內采用不放回簡單隨機抽樣）從甲、乙兩組共抽取4名工人進行技術考核．
（1）求從甲、乙兩組各抽取的人數；
（2）求從甲組抽取的工人中恰有1名女工人的概率；
（3）求抽取的4名工人中恰有2名男工人的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
