【題目】把函數y=cos2x+ 
sin2x的圖象向左平移m（其中m＞0）個單位，所得圖象關于y軸對稱，則m的最小值是（ ）
A.
B.
C.
D.
【答案】B
【解析】解：把函數y=cos2x+ 
sin2x=2sin（2x+ 
）的圖象向左平移m（其中m＞0）個單位，可得y=2sin[2（x+m）+ ]=2sin（2x+2m+ ）的圖象，
所得圖象關于y軸對稱，則2m+ =kπ+ 
，k∈Z，即 m=kπ+ ，故正數m的最小值是 ，
故選：B．
【考點精析】解答此題的關鍵在于理解函數y=Asin（ωx+φ）的圖象變換的相關知識，掌握圖象上所有點向左（右）平移
個單位長度，得到函數
的圖象；再將函數的圖象上所有點的橫坐標伸長（縮短）到原來的
倍（縱坐標不變），得到函數
的圖象；再將函數的圖象上所有點的縱坐標伸長（縮短）到原來的
倍（橫坐標不變），得到函數
的圖象．
第1卷單元月考期中期末系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓
的一個焦點為
，且離心率為
．
（1）求橢圓方程；
（2）斜率為
的直線
過點
，且與橢圓交于
兩點， 
為直線
上的一點，若△
為等邊三角形，求直線
的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知a，b，c分別是△ABC內角A，B，C的對邊，sin2B=2sinAsinC．
（Ⅰ）若a=b，求cosB；
（Ⅱ）設B=90°，且a=
， 求△ABC的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司研究開發了一種新產品，生產這種新產品的年固定成本為150萬元，每生產
千件，需另投入成本為
(萬元)，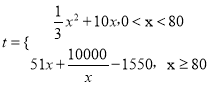 
.每件產品售價為500元.該新產品在市場上供不應求可全部賣完.
（Ⅰ）寫出年利潤
（萬元）關于年產量
（千件）的函數解析式；
（Ⅱ）當年產量為多少千件時，該公司在這一新產品的生產中所獲利潤最大.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x2﹣mx+m，m、x∈R．
（1）若關于x的不等式f（x）＞0的解集為R，求m的取值范圍；
（2）若實x1 ， x2數滿足x1＜x2 ， 且f（x1）≠f（x2），證明：方程f（x）= 
[f（x1）+f（x2）]至少有一個實根x0∈（x1 ， x2）；
（3）設F（x）=f（x）+1﹣m﹣m2 ， 且|F（x）|在[0，1]上單調遞增，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】空氣質量主要受污染物排放量及大氣擴散等因素的影響，某市環保監測站2014年10月連續10天（從左到右對應1號至10號）采集該市某地平均風速及空氣中氧化物的日均濃度數據，制成散點圖如圖所示．
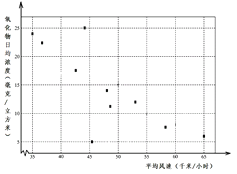
（Ⅰ）同學甲從這10天中隨機抽取連續5天的一組數據，計算回歸直線方程．試求連續5天的一組數據中恰好同時包含氧化物日均濃度最大與最小值的概率；
（Ⅱ）現有30名學生，每人任取5天數據，對應計算出30個不同的回歸直線方程．已知30組數據中有包含氧化物日均濃度最值的有14組．現采用這30個回歸方程對某一天平均風速下的氧化物日均濃度進行預測，若預測值與實測值差的絕對值小于2，則稱之為“擬合效果好”，否則為“擬合效果不好”．根據以上信息完成下列2×2聯表，并分析是否有95%以上的把握說擬合效果與選取數據是否包含氧化物日均濃度最值有關．
預測效果好 | 擬合效果不好 | 合計 | |
數據有包含最值 | 5 | ||
數據無包含最值 | 4 | ||
合計 |
參考數據：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
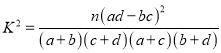（其中
）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐ABCD﹣PGFE中，底面ABCD是直角梯形，側棱垂直于底面，AB∥DC，∠ABC=45°，DC=1，AB=2，PA=1．
（Ⅰ）求PD與BC所成角的大小；
（Ⅱ）求證：BC⊥平面PAC；
（Ⅲ）求二面角A﹣PC﹣D的大小．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
