
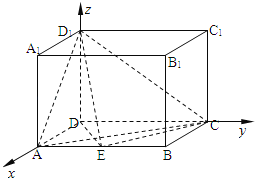
【題目】如圖,長方體ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,點E是線段AB中點.

(1)證明:D1E⊥CE;
(2)求二面角D1﹣EC﹣D的大小的余弦值;
(3)求A點到平面CD1E的距離.
【答案】(1)見解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據線面垂直的性質定理,證明CE⊥面D1DE即可證明:D1E⊥CE;
(2)建立坐標系,利用向量法即可求二面角D1﹣EC﹣D的大小的余弦值;
(3)根據點到平面的距離公式,即可求A點到平面CD1E的距離.
(1)證明:DD1⊥面ABCD,CE面ABCD;
所以DD1⊥CE,
Rt△DAE中,AD=1,AE=1,
DE![]() ,
,
同理:CE![]() ,又CD=2,CD2=CE2+DE2,
,又CD=2,CD2=CE2+DE2,
DE⊥CE,
DE∩CE=E,
所以,CE⊥面D1DE,
又D1E面D1EC,
所以,D1E⊥CE;
(2)設平面CD1E的法向量為![]() (x,y,z),
(x,y,z),
由(1)得![]() (1,1,﹣1),
(1,1,﹣1),![]() (1,﹣1,0)
(1,﹣1,0)
![]()
![]() x+y﹣1=0,
x+y﹣1=0,![]()
![]() x﹣y=0
x﹣y=0
解得:x=y![]() ,即
,即![]() (
(![]() ,
,![]() ,1);
,1);
又平面CDE的法向量為![]() (0,0,1),
(0,0,1),
∴cos![]() ,
,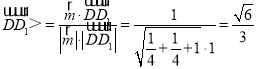 span>,
span>,
所以,二面角D1﹣EC﹣D的余弦值為![]() ;
;
(3)由(1)(2)知![]() (0,1,0),平面CD1E的法向量為
(0,1,0),平面CD1E的法向量為![]() (
(![]() ,
,![]() ,1);
,1);
故A點到平面CD1E的距離為d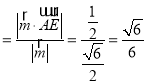 .
.


科目:高中數學 來源: 題型:
【題目】某市有兩家共享單車公司,在市場上分別投放了黃、藍兩種顏色的單車,已知黃、藍兩種顏色的單車的投放比例為2:1.監管部門為了了解兩種顏色的單車的質量,決定從市場中隨機抽取5輛單車進行體驗,若每輛單車被抽取的可能性相同.
(1)求抽取的5輛單車中有2輛是藍色顏色單車的概率;
(2)在騎行體驗過程中,發現藍色單車存在一定質量問題,監管部門決定從市場中隨機地抽取一輛送技術部門作進一步抽樣檢測,并規定若抽到的是藍色單車,則抽樣結束,若抽取的是黃色單車,則將其放回市場中,并繼續從市場中隨機地抽取下一輛單車,并規定抽樣的次數最多不超過![]() (
(![]() )次.在抽樣結束時,已取到的黃色單車以
)次.在抽樣結束時,已取到的黃色單車以![]() 表示,求
表示,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 、
、![]() 是異面直線,給出下列結論:
是異面直線,給出下列結論:
①一定存在平面![]() ,使直線
,使直線![]() 平面
平面![]() ,直線
,直線![]() 平面
平面![]() ;
;
②一定存在平面![]() ,使直線
,使直線![]() 平面
平面![]() ,直線
,直線![]() 平面
平面![]() ;
;
③一定存在無數個平面![]() ,使直線
,使直線![]() 與平面
與平面![]() 交于一個定點,且直線
交于一個定點,且直線![]() 平面
平面![]() .
.
則所有正確結論的序號為( )
A.①②B.②C.②③D.③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左頂點為
的左頂點為![]() ,右焦點為
,右焦點為![]() ,過
,過![]() 作垂直于
作垂直于![]() 軸的直線交該橢圓于
軸的直線交該橢圓于![]() ,
,![]() 兩點,直線
兩點,直線![]() 的斜率為
的斜率為![]() .
.
(Ⅰ)求橢圓的離心率;
(Ⅱ)若![]() 的外接圓在
的外接圓在![]() 處的切線與橢圓交另一點于
處的切線與橢圓交另一點于![]() ,且
,且![]() 的面積為
的面積為![]() ,求橢圓的方程.
,求橢圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】保護環境,防治環境污染越來越得到人們的重視,某企業在現有設備下每日生產總成本![]() (單位:萬元)與日產量
(單位:萬元)與日產量![]() (單位:噸)之間的函數關系式為
(單位:噸)之間的函數關系式為![]() .現為了減少大氣污染,該企業引進了除塵設備,每噸產品除塵費用為
.現為了減少大氣污染,該企業引進了除塵設備,每噸產品除塵費用為![]() 萬元,除塵后,當日產量
萬元,除塵后,當日產量![]() 時,每日生產總成本
時,每日生產總成本![]() .
.
(1)求![]() 的值;
的值;
(2)若每噸產品出廠價為48萬元,試求除塵后日產量為多少噸時,每噸產品的利潤最大,最大利潤為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
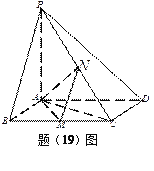
【題目】(本小題滿分12分)
如圖,已知四棱錐![]() ,底面
,底面![]() 為菱形,
為菱形,![]() ,
,
![]() ,
, ![]() 平面
平面![]() ,
, ![]() 分別是
分別是![]() 的中點。
的中點。
(1)證明: ![]() ;
;
(2)若![]() 為
為![]() 上的動點,
上的動點,![]() 與平面
與平面![]() 所成最大角
所成最大角
的正切值為![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com