
【題目】已知![]() 中,角
中,角![]() 所對的邊分別為
所對的邊分別為![]() ,滿足
,滿足![]() .
.
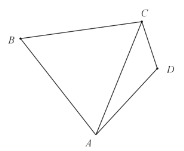
(1)求![]() 的大小;
的大小;
(2)如圖,![]() ,在直線
,在直線![]() 的右側取點
的右側取點![]() ,使得
,使得![]() .當角
.當角![]() 為何值時,四邊形
為何值時,四邊形![]() 面積最大.
面積最大.
科目:高中數學 來源: 題型:
【題目】為了美化環境,某公園欲將一塊空地規劃建成休閑草坪,休閑草坪的形狀為如圖所示的四邊形ABCD.其中AB=3百米,AD=![]() 百米,且△BCD是以D為直角頂點的等腰直角三角形.擬修建兩條小路AC,BD(路的寬度忽略不計),設∠BAD=
百米,且△BCD是以D為直角頂點的等腰直角三角形.擬修建兩條小路AC,BD(路的寬度忽略不計),設∠BAD=![]() ,
,![]() (
(![]() ,
,![]() ).
).
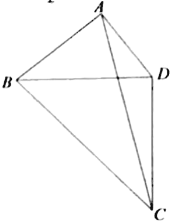
(1)當cos![]() =
=![]() 時,求小路AC的長度;
時,求小路AC的長度;
(2)當草坪ABCD的面積最大時,求此時小路BD的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
:![]() ,直線
,直線![]() .
.
(1)若直線![]() 與圓
與圓![]() 相切,求
相切,求![]() 的值;
的值;
(2)若直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() ,當∠AOB為銳角時,求k的取值范圍;
,當∠AOB為銳角時,求k的取值范圍;
(3)若![]() ,
,![]() 是直線
是直線![]() 上的動點,過
上的動點,過![]() 作圓
作圓![]() 的兩條切線
的兩條切線![]() ,切點為
,切點為![]() ,探究:直線
,探究:直線![]() 是否過定點。
是否過定點。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從高一年級期末考試的學生中抽出 6![]() 名學生,其成績(均為整數)的頻率分布直方圖如圖所示.
名學生,其成績(均為整數)的頻率分布直方圖如圖所示.
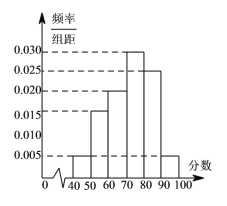
(1)估計這次考試的中位數
(2)假設分數在![]() 的學生的成績都不相同,且都在
的學生的成績都不相同,且都在![]() 分以上,現用簡單隨機抽樣方法,從
分以上,現用簡單隨機抽樣方法,從![]() 這
這 ![]() 個數中任取
個數中任取 ![]() 個數,求這
個數,求這 ![]() 個數恰好是兩個學生的成績的概率.
個數恰好是兩個學生的成績的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在長方體ABCD-A1B1C1D1中,AB=2,BC=2,CC1=3,長方體每條棱所在直線與過點C1的平面α所成的角都相等,則直線AC與平面α所成角的余弦值為( )
A. ![]() 或1 B.
或1 B. ![]() 或0 C.
或0 C. ![]() 或0 D.
或0 D. ![]() 或1
或1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是一個幾何體的平面展開圖,其中四邊形ABCD為正方形,△PDC, △PBC, △PAB, △PDA為全等的等邊三角形,E、F分別為PA、PD的中點,在此幾何體中,下列結論中錯誤的為 ( )

A. 平面BCD⊥平面PAD B. 直線BE與直線AF是異面直線
C. 直線BE與直線CF共面 D. 面PAD與面PBC的交線與BC平行
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com