
【題目】某共享單車經營企業欲向甲市投放單車,為制定適宜的經營策略,該企業首先在已投放單車的乙市進行單車使用情況調查.調查過程分隨機問卷、整理分析及開座談會三個階段.在隨機問卷階段,![]() ,
,![]() 兩個調查小組分赴全市不同區域發放問卷并及時收回;在整理分析階段,兩個調查小組從所獲取的有效問卷中,針對15至45歲的人群,按比例隨機抽取了300份,進行了數據統計,具體情況如下表:
兩個調查小組分赴全市不同區域發放問卷并及時收回;在整理分析階段,兩個調查小組從所獲取的有效問卷中,針對15至45歲的人群,按比例隨機抽取了300份,進行了數據統計,具體情況如下表:
組別 年齡 |
|
| ||
經常使用單車 | 偶爾使用單車 | 經常使用單車 | 偶爾使用單車 | |
| 27人 | 13人 | 40人 | 20人 |
| 23人 | 17人 | 35人 | 25人 |
| 20人 | 20人 | 35人 | 25人 |
(1)先用分層抽樣的方法從上述300人中按“年齡是否達到35歲”抽出一個容量為60人的樣本,再用分層抽樣的方法將“年齡達到35歲”的被抽個體數分配到“經常使用單車”和“偶爾使用單車”中去.
①求這60人中“年齡達到35歲且偶爾使用單車”的人數;
②為聽取對發展共享單車的建議,調查組專門組織所抽取的“年齡達到35歲且偶爾使用單車”的人員召開座談會.會后共有3份禮品贈送給其中3人,每人1份(其余人員僅贈送騎行優惠券).已知參加座談會的人員中有且只有4人來自![]() 組,求
組,求![]() 組這4人中得到禮品的人數
組這4人中得到禮品的人數![]() 的分布列和數學期望;
的分布列和數學期望;
(2)從統計數據可直觀得出“是否經常使用共享單車與年齡(記作![]() 歲)有關”的結論.在用獨立性檢驗的方法說明該結論成立時,為使犯錯誤的概率盡可能小,年齡
歲)有關”的結論.在用獨立性檢驗的方法說明該結論成立時,為使犯錯誤的概率盡可能小,年齡![]() 應取25還是35?請通過比較
應取25還是35?請通過比較![]() 的觀測值的大小加以說明.
的觀測值的大小加以說明.
參考公式: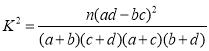 ,其中
,其中![]() .
.
【答案】(1) ①9人 ②見解析;(2) ![]()
【解析】
(1)①根據分層抽樣要求,先求從300人中抽取60人,其中“年齡達到35歲”的人數![]() ,再求“年齡達到35歲” 中偶爾使用單車的人數
,再求“年齡達到35歲” 中偶爾使用單車的人數![]() ;
;
②確定隨機變量X的取值,計算X各個取值的概率,得分布列及數學期望.
(2)對年齡m是否達到35,m是否達到25對數據重新整理(2![]() 2聯表),根據公式計算相應的
2聯表),根據公式計算相應的![]() ,比較大小確定.
,比較大小確定.
(1)①從300人中抽取60人,其中“年齡達到35歲”的有![]() 人,再將這20人用分層抽樣法按“是否經常使用單車”進行名額劃分,其中“年齡達到35歲且偶爾使用單車”的人數為
人,再將這20人用分層抽樣法按“是否經常使用單車”進行名額劃分,其中“年齡達到35歲且偶爾使用單車”的人數為![]() .
.
②![]() 組這4人中得到禮品的人數
組這4人中得到禮品的人數![]() 的可能取值為0,1,2,3,相應概率為:
的可能取值為0,1,2,3,相應概率為:
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
故其分布列為
| 0 | 1 | 2 | 3 |
|
|
|
|
|
∴![]() .
.
(2)按“年齡是否達到35歲”對數據進行整理,得到如下列聯表:
經常使用單車 | 偶爾使用單車 | 合計 | |
未達到35歲 | 125 | 75 | 200 |
達到35歲 | 55 | 45 | 100 |
合計 | 180 | 120 | 300 |
![]() 時,由(1)中的列聯表,可求得
時,由(1)中的列聯表,可求得![]() 的觀測值
的觀測值
![]() .
.
![]() 時,按“年齡是否達到25歲”對數據進行整理,得到如下列聯表:
時,按“年齡是否達到25歲”對數據進行整理,得到如下列聯表:
經常使用單車 | 偶爾使用單車 | 合計 | |
未達到25歲 | 67 | 33 | 100 |
達到25歲 | 113 | 87 | 200 |
合計 | 180 | 120 | 300 |
可求得![]() 的觀測值
的觀測值
![]() .
.
∴![]() ,
,
欲使犯錯誤的概率盡可能小,需取![]() .
.


科目:高中數學 來源: 題型:
【題目】某百貨商店今年春節期間舉行促銷活動,規定消費達到一定標準的顧客可進行一次抽獎活動,隨著抽獎活動的有效開展,參與抽獎活動的人數越來越多,該商店經理對春節前![]() 天參加抽獎活動的人數進行統計,
天參加抽獎活動的人數進行統計,![]() 表示第
表示第![]() 天參加抽獎活動的人數,得到統計表格如下:
天參加抽獎活動的人數,得到統計表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
(1)經過進一步統計分析,發現![]() 與
與![]() 具有線性相關關系.請根據上表提供的數據,用最小二乘法求出
具有線性相關關系.請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)該商店規定:若抽中“一等獎”,可領取600元購物券;抽中“二等獎”可領取300元購物券;抽中“謝謝惠顧”,則沒有購物券.已知一次抽獎活動獲得“一等獎”的概率為![]() ,獲得“二等獎”的概率為
,獲得“二等獎”的概率為![]() .現有張、王兩位先生參與了本次活動,且他們是否中獎相互獨立,求此二人所獲購物券總金額
.現有張、王兩位先生參與了本次活動,且他們是否中獎相互獨立,求此二人所獲購物券總金額![]() 的分布列及數學期望.
的分布列及數學期望.
參考公式:,
![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,四點
,四點![]() 、
、![]() 、
、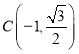 、
、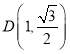 中恰有三點在橢圓上.
中恰有三點在橢圓上.
(1)求橢圓的方程;
(2)已知點![]() 是橢圓的右頂點,作一條平行于
是橢圓的右頂點,作一條平行于![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 、
、![]() 兩點,記直線
兩點,記直線![]() 和直線
和直線![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,試判斷
,試判斷![]() 是否為定值?若是,求出該定值;若不是,請說明理由.
是否為定值?若是,求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數![]() 有下述四個結論:
有下述四個結論:
①![]() 是偶函數;②
是偶函數;②![]() 在區間
在區間![]() 單調遞減;
單調遞減;
③![]() 在
在![]() 有
有![]() 個零點;④
個零點;④![]() 的最大值為
的最大值為![]() .
.
其中所有正確結論的編號是( )
A.①②④B.②④C.①④D.①③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】氣象意義上,從春季進入夏季的標志為:“連續5天的日平均溫度不低于22℃”.現有甲、乙、丙三地連續5天的日平均溫度的記錄數據(記錄數據都是正整數):
①甲地:5個數據的中位數為24,眾數為22;
②乙地:5個數據的中位數為27,總體均值為24;
③丙地:5個數據的中有一個數據是32,總體均值為26,總體方差為10.8;
則肯定進入夏季的地區的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為慶祝新中國成立七十周年,巴蜀中學將舉行“歌唱祖國,喜迎國慶”歌詠比賽活動,《歌唱祖國》,《精忠報國》,《我和我的祖國》等一系列歌曲深受同學們的青睞,高二某班級就該班是否選擇《精忠報國》作為本班參賽曲目進行投票表決,投票情況如下表.
小組 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
贊成人數 | 4 | 5 | 6 | 6 | 5 | 6 | 4 | 3 |
總人數 | 7 | 7 | 8 | 8 | 7 | 7 | 6 | 6 |
(1)若從第1小組和第8小組的同學中各隨機選取2人進行調查,求所選取的4人中至少有2人贊成《精忠報國》作為本班參賽曲目的概率;
(2)若從第5小組和第7小組的同學中各隨機選取2人進行調查,記選取的4人中不贊成《精忠報國》作為本班參賽曲目的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com