
【題目】已知實數![]() ,設函數
,設函數![]()
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)對任意![]() 均有
均有![]() 求
求![]() 的取值范圍.
的取值范圍.
注:![]() 為自然對數的底數.
為自然對數的底數.
【答案】(1)![]() 的單調遞增區間是
的單調遞增區間是![]() ,單調遞減區間是
,單調遞減區間是![]() ;(2)
;(2)![]() .
.
【解析】
(1)首先求得導函數的解析式,然后結合函數的解析式確定函數的單調區間即可.
(2)由題意首先由函數在特殊點的函數值得到a的取值范圍,然后證明所得的范圍滿足題意即可.
(1)當![]() 時,
時,![]() ,函數的定義域為
,函數的定義域為![]() ,且:
,且:
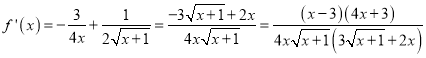 ,
,
因此函數![]() 的單調遞增區間是
的單調遞增區間是![]() ,單調遞減區間是
,單調遞減區間是![]() .
.
(2)構造函數![]() ,
,
注意到:![]() ,
,
注意到![]() 時
時![]() 恒成立,滿足
恒成立,滿足![]() ;
;
當![]() 時,
時,![]() ,不合題意,
,不合題意,
且![]() ,解得:
,解得:![]() ,故
,故![]() .
.
下面證明![]() 剛好是滿足題意的實數a的取值范圍.
剛好是滿足題意的實數a的取值范圍.
分類討論:
(a)當![]() 時,
時,![]() ,
,
令![]() ,則:
,則:
![]()
![]()

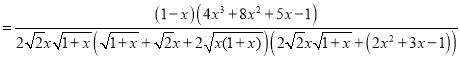 ,
,
易知![]() ,則函數
,則函數![]() 單調遞減,
單調遞減,![]() ,滿足題意.
,滿足題意.
(b)當![]() 時,
時,![]() 等價于
等價于![]() ,
,
左側是關于a的開口向下的二次函數![]() ,
,
其判別式![]() ,
,
令![]() ,注意到當
,注意到當![]() 時,
時,![]() ,
,
于是![]() 在
在![]() 上單調遞增,而
上單調遞增,而![]() ,
,
于是當![]() 時命題成立,
時命題成立,
而當![]() 時,此時
時,此時![]() 的對稱軸為
的對稱軸為![]() 隨著
隨著![]() 遞增,
遞增,
于是對稱軸在![]() 的右側,而
的右側,而![]() 成立,(不等式等價于
成立,(不等式等價于![]() ).
).
因此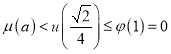 .
.
綜上可得:實數a的取值范圍是![]() .
.


 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:高中數學 來源: 題型:
【題目】已知![]() ,直線
,直線![]() 分別交
分別交![]() 軸、
軸、![]() 軸的正半軸于
軸的正半軸于![]() 、
、![]() 兩點,
兩點,![]() 為坐標原點.
為坐標原點.
(1)若直線![]() 方程為
方程為![]() (
(![]() ),且
),且![]() ,求
,求![]() 的值;
的值;
(2)若直線![]() 經過點
經過點![]() ,設
,設![]() 的斜率為
的斜率為![]() ,
,![]() 為線段
為線段![]() 的中點,求
的中點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知不共線向量![]() ,
,![]() 滿足|
滿足|![]() |=3,|
|=3,|![]() |=2,(2
|=2,(2![]() 3
3![]() )(2
)(2![]() )=20.
)=20.
(1)求![]()
![]() ;
;
(2)是否存在實數λ,使λ![]() 與
與![]() 2
2![]() 共線?
共線?
(3)若(k![]() 2
2![]() )⊥(
)⊥(![]() ),求實數k的值.
),求實數k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
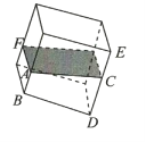
【題目】在一個長方體的容器中,里面裝有少量的水,現在將容器繞著其底部的一條棱傾斜.
(1)在傾斜的過程中,水面的形狀不斷變化,可能是矩形,也可能變成不是矩形的平行四邊形,對嗎?
(2)在傾斜的過程中,水的形狀也不斷變化,可以是棱柱,也可能變為棱臺或棱錐,對嗎?
(3)如果傾斜時,不是繞著底部的一條棱,而是繞著其底面的一個頂點,上面的第(1)問和第(2)問對不對?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動點P與兩個定點O(0,0),A(3,0)的距離的比值為2,點P的軌跡為曲線C.
(1)求曲線C的軌跡方程
(2)過點(﹣1,0)作直線與曲線C交于A,B兩點,設點M坐標為(4,0),求△ABM面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在△![]() 中,
中,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,![]() 為
為![]() 的中點,
的中點, ![]() ,
,![]() .將△
.將△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
, ![]() 為
為![]() 的中點,如圖2.
的中點,如圖2.
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求F到平面A1OB的距離.

圖1 圖2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com