
【題目】已知正項等比數列{an}滿足a1 , 2a2 , a3+6成等差數列,且a42=9a1a5 ,
(1)求數列{an}的通項公式;
(2)設bn=( ![]() an+1)an , 求數列{bn}的前n項和Tn .
an+1)an , 求數列{bn}的前n項和Tn .
【答案】
(1)解:設正項等比數列{an}的公比為q>0,∵a1,2a2,a3+6成等差數列,∴2×2a2=a3+6+a1,又a42=9a1a5,
∴ 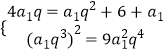 ,解得a1=q=3.
,解得a1=q=3.
∴an=3n.
(2)解:bn=( ![]() an+1)an=(2n+1)3n.
an+1)an=(2n+1)3n.
∴數列{bn}的前n項和Tn=3×3+5×32+…+(2n+1)3n.
3Tn=3×32+5×33+…+(2n﹣1)3n+(2n+1)3n+1,
∴﹣2Tn=32+2×(32+33+…+3n)﹣(2n+1)3n+1= ![]() +3﹣(2n+1)3n+1=﹣2n3n+1,
+3﹣(2n+1)3n+1=﹣2n3n+1,
∴Tn=n3n+1.
【解析】(1)利用等差數列與等比數列的通項公式即可得出.(2)bn=( ![]() an+1)an=(2n+1)3n . 再利用“錯位相減法”與等比數列的前n項和公式即可得出.
an+1)an=(2n+1)3n . 再利用“錯位相減法”與等比數列的前n項和公式即可得出.
【考點精析】掌握數列的前n項和和數列的通項公式是解答本題的根本,需要知道數列{an}的前n項和sn與通項an的關系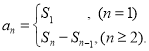 ;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.
;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.


科目:高中數學 來源: 題型:
【題目】某科研課題組通過一款手機APP軟件,調查了某市1000名跑步愛好者平均每周的跑步量(簡稱“周跑量”),得到如下的頻數分布表
周跑量(km/周) |
|
|
|
|
|
|
|
|
|
人數 | 100 | 120 | 130 | 180 | 220 | 150 | 60 | 30 | 10 |
(1)在答題卡上補全該市1000名跑步愛好者周跑量的頻率分布直方圖:
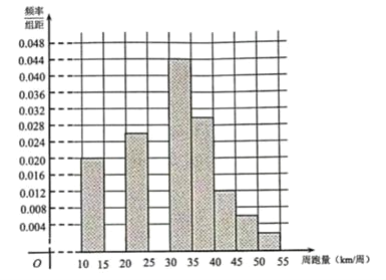
注:請先用鉛筆畫,確定后再用黑色水筆描黑
(2)根據以上圖表數據計算得樣本的平均數為![]() ,試求樣本的中位數(保留一位小數),并用平均數、中位數等數字特征估計該市跑步愛好者周跑量的分布特點
,試求樣本的中位數(保留一位小數),并用平均數、中位數等數字特征估計該市跑步愛好者周跑量的分布特點
(3)根據跑步愛好者的周跑量,將跑步愛好者分成以下三類,不同類別的跑者購買的裝備的價格不一樣,如下表:
周跑量 | 小于20公里 | 20公里到40公里 | 不小于40公里 |
類別 | 休閑跑者 | 核心跑者 | 精英跑者 |
裝備價格(單位:元) | 2500 | 4000 | 4500 |
根據以上數據,估計該市每位跑步愛好者購買裝備,平均需要花費多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一元二次函數的最大值為![]() ,其圖象的對稱軸為
,其圖象的對稱軸為![]() ,且與
,且與![]() 軸兩個交點的橫坐標的平方和為
軸兩個交點的橫坐標的平方和為![]() .
.
(1)求該一元二次函數;
(2)要將該函數圖象的頂點平移到原點,請說出平移的方式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為線段
分別為線段![]() 上的點,且
上的點,且![]() ,
, ![]() ,
, ![]() .
.
(1)求證: ![]() 平面
平面![]() ;
;
(2)若![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成的銳二面角.
所成的銳二面角.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中, 已知圓
中, 已知圓![]()
![]() ,橢圓
,橢圓![]()
![]() ,
,![]() 為橢圓右頂點.過原點
為橢圓右頂點.過原點![]() 且異于坐標軸的直線與橢圓
且異于坐標軸的直線與橢圓![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 與圓
與圓![]() 的另一交點為
的另一交點為![]() ,直線
,直線![]() 與圓
與圓![]() 的另一交點為
的另一交點為![]() ,其中
,其中![]() .設直線
.設直線![]() 的斜率分別為
的斜率分別為![]() .
.

(1)求![]() 的值;
的值;
(2)記直線![]() 的斜率分別為
的斜率分別為![]() ,是否存在常數
,是否存在常數![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 值;若不存在,說明理由;
值;若不存在,說明理由;
(3)求證:直線![]() 必過點
必過點![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】二項式![]() 的展開式中只有第6項的二項式系數最大,且展開式中的第3項的系數是第4項的系數的3倍,則
的展開式中只有第6項的二項式系數最大,且展開式中的第3項的系數是第4項的系數的3倍,則![]() 的值為( )
的值為( )
A. 4 B. 8 C. 12 D. 16
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,與
,與![]() 軸正半軸交于點
軸正半軸交于點![]() ,若
,若![]() 為等腰直角三角形,且直線
為等腰直角三角形,且直線![]() 被圓
被圓![]() 所截得的弦長為2.
所截得的弦長為2.
(1)求橢圓的方程;
(2)直線![]() :
:![]() 與橢圓交于點
與橢圓交于點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,射線
,射線![]() 與橢圓交于點
與橢圓交于點![]() ,點
,點![]() 為
為![]() 的重心,求證:
的重心,求證:![]() 的面積
的面積![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,若a,b,c∈R,f(a),f(b),f(c)為某一個三角形的邊長,則實數m的取值范圍是( )
,若a,b,c∈R,f(a),f(b),f(c)為某一個三角形的邊長,則實數m的取值范圍是( )
A.[ ![]() ,1]
,1]
B.[0,1]
C.[1,2]
D.[ ![]() ,2]
,2]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com