Question

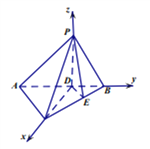
【題目】如圖，在三棱錐中，平面平面， ， ， ， 分別為線段上的點，且， ， .

（1）求證： 平面；

（2）若與平面所成的角為，求平面與平面所成的銳二面角.

Answer 1

【答案】(1)證明見解析；(2)30°.

【解析】試題分析：

（1）由條件可得為直角三角形，且．故由余弦定理可得，所以，從而，又由條件可得，故平面．（2）由兩兩互相垂直可建立空間直角坐標系，結合條件可求得平面的法向量和平面的法向量，根據兩法向量夾角的余弦值可得銳二面角的大小．

試題解析：

（1）證明：連，由題意知．

∴

在中，由余弦定理得

,

∴,

∴,

又因為，

∴

又 ，

又， ，

∴平面．

（2）由（1）知兩兩互相垂直，建立如圖所示的空間直角坐標系，

由與平面所成的角為，知，

則

∴

因為

由（1）知 平面，

∴平面

∴為平面的一個法向量.

設平面的法向量為，

則 ∴，

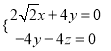令，則，

∴為平面的一個法向量.

∴

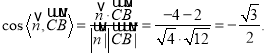
故平面與平面的銳二面角的余弦值為,

所以平面與平面的銳二面角為．