
【題目】如圖所示,等腰![]() 的底邊
的底邊![]() ,高
,高![]() ,點
,點![]() 是線段
是線段![]() 上異于點
上異于點![]() 的動點,點
的動點,點![]() 在
在![]() 邊上,且
邊上,且![]() ,現沿
,現沿![]() 將△
將△![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() ,記
,記![]() ,
, ![]() 表示四棱錐
表示四棱錐![]() 的體積.
的體積.
(1)求![]() 的表達式;(2)當
的表達式;(2)當![]() 為何值時,
為何值時, ![]() 取得最大,并求最大值。
取得最大,并求最大值。
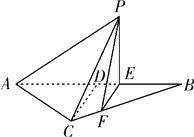
【答案】(1) VP-ACFE=![]() (2)
(2) ![]()
![]()
【解析】試題分析:(1)![]() ,S四邊形ACFE=S△ABC-S△BEF=
,S四邊形ACFE=S△ABC-S△BEF=![]() ,所以四棱錐P-ACFE的體積VP-ACFE=
,所以四棱錐P-ACFE的體積VP-ACFE=![]() S四邊形ACFE·PE=
S四邊形ACFE·PE=![]() ;(2)V′(x)=0
;(2)V′(x)=0 ![]() ,所以
,所以![]()
![]() 。
。
試題解析:
(1)因為EF⊥AB,所以EF⊥PE.又因為PE⊥AE,EF∩AE=E,所以PE⊥平面ACFE. 因為EF⊥AB,CD⊥AB,且CD,EF共面,所以EF∥CD,
所以![]()
![]()
所以四邊形ACFE的面積
S四邊形ACFE=S△ABC-S△BEF=![]()
所以四棱錐P-ACFE的體積VP-ACFE=![]() S四邊形ACFE·PE=
S四邊形ACFE·PE=![]()
(2)由(1)知. ![]() 令V′(x)=0
令V′(x)=0 ![]() 因為當
因為當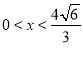 時,V′(x)>0, 當
時,V′(x)>0, 當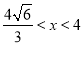 時,V′(x)<0.所以當
時,V′(x)<0.所以當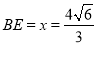 時,
時, 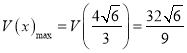


科目:高中數學 來源: 題型:
【題目】一牧羊人趕著一群羊通過4個關口,每過一個關口,守關人將拿走當時羊的一半,然后退還一只給牧羊人,過完這些關口后,牧羊人只剩下3只羊,則牧羊人在過第1個關口前有_________只羊.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,則下列命題中正確的個數是( )
,則下列命題中正確的個數是( )
①當![]() 時,函數
時,函數![]() 在
在![]() 上是單調增函數;
上是單調增函數;
②當![]() 時,函數
時,函數![]() 在
在![]() 上有最小值;
上有最小值;
③函數![]() 的圖象關于點
的圖象關于點![]() 對稱;
對稱;
④方程![]() 可能有三個實數根.
可能有三個實數根.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知cos(75°+α)=![]() ,α是第三象限角,
,α是第三象限角,
(1)求sin(75°+α) 的值.
(2)求cos(α-15°) 的值.
(3)求sin(195°-α)+cos(105o-α)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,若在定義域內存在
,若在定義域內存在![]() ,使得
,使得![]() 成立,則稱
成立,則稱![]() 為函數
為函數![]() 的局部對稱點.
的局部對稱點.
(1)若![]() ,證明:函數
,證明:函數![]() 必有局部對稱點;
必有局部對稱點;
(2)若函數![]() 在區間
在區間![]() 內有局部對稱點,求實數
內有局部對稱點,求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() 在
在![]() 上有局部對稱點,求實數
上有局部對稱點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com