Question

【題目】如圖，在四棱錐P﹣ABCD中，底面ABCD為正方形，PA⊥底面ABCD，AD=AP，E為棱PD中點．
（1）求證：PD⊥平面ABE；
（2）若F為AB中點， ，試確定λ的值，使二面角P﹣FM﹣B的余弦值為 ．

Answer 1

【答案】
（1）證明：∵PA⊥底面ABCD，AB底面ABCD，∴PA⊥AB，

又∵底面ABCD為矩形，∴AB⊥AD，PA∩AD=A，PA平面PAD，AD平面PAD，

∴AB⊥平面PAD，又PD平面PAD，∴AB⊥PD，AD=AP，E為PD中點，∴AE⊥PD，AE∩AB=A，AE平面ABE，AB平面ABE，∴PD⊥平面ABE

（2）解：以A為原點，以 為x，y，z軸正方向，建立空間直角坐標系A﹣BDP，令|AB|=2，

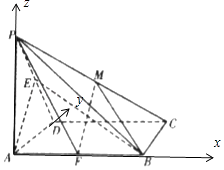
則A（0，0，0），B（2，0，0），P（0，0，2），C（2，2，0），E（0，1，1），F（1，0，0）， ， ， ，M（2λ，2λ，2﹣2λ）

設平面PFM的法向量 ， ，即 ，

設平面BFM的法向量 ， ，

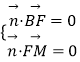即 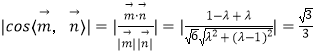， ，解得

【解析】（I）證明AB⊥平面PAD，推出AB⊥PD，AE⊥PD，AE∩AB=A，即可證明PD⊥平面ABE．（II） 以A為原點，以 為x，y，z軸正方向，建立空間直角坐標系A﹣BDP，求出相關點的坐標，平面PFM的法向量，平面BFM的法向量，利用空間向量的數量積求解即可．