
【題目】某市英才中學的一個社會實踐調查小組,在對中學生的良好“光盤習慣”的調查中,隨機發(fā)放了120份問卷,對收回的120份有效問卷進行統(tǒng)計,得到如下![]() 列聯(lián)表:
列聯(lián)表:
做不到光盤 | 能做到光盤 | 合計 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合計 | 75 | 25 | 100 |
(1)現已按是否能做到光盤分層從45份女生問卷中抽取9份問卷,若從這9份問卷中隨機抽取4份,并記其中能做到光盤的問卷的份數為![]() ,試求隨機變量
,試求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(2)如果認為良好“光盤習慣”與性別有關犯錯誤的概率不超過![]() ,那么根據臨界值表最精確的
,那么根據臨界值表最精確的![]() 的值應為多少?請說明理由.
的值應為多少?請說明理由.
附:獨立性檢驗統(tǒng)計量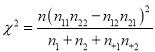 ,其中
,其中![]() .
.
獨立性檢驗臨界表:
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)詳見解析;(2)![]() .
.
【解析】試題分析:(1)先確定![]() 的可能取值有0,1,2,3,算出其概率分別為:
的可能取值有0,1,2,3,算出其概率分別為:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .再求出其分布列,算出其數學期望
.再求出其分布列,算出其數學期望![]() ;(2)依據題設中提供的2
;(2)依據題設中提供的2![]() 2聯(lián)列表中的數據算出
2聯(lián)列表中的數據算出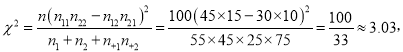 再與獨立性檢驗臨界表中的數據進行比對,從而做出判斷。
再與獨立性檢驗臨界表中的數據進行比對,從而做出判斷。
試題解析:
(1)因為9份女生問卷是用分層抽樣方法取得的,所以9份問卷中有6份做不到光盤,3份能做到光盤,因為![]() 表示從這9份問卷中隨機抽出的4分中能做到光盤的問卷數,所以
表示從這9份問卷中隨機抽出的4分中能做到光盤的問卷數,所以![]() 的可能取值有0,1,2,3,其概率分別為:
的可能取值有0,1,2,3,其概率分別為:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
隨機變量![]() 分布列如下:
分布列如下:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() .
.
(2) 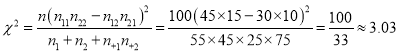 .
.
因為![]() ,所以能在犯錯誤的概率不超過
,所以能在犯錯誤的概率不超過![]() 的前提下認為良好“光盤習慣”與性別有關,即精確的值應為
的前提下認為良好“光盤習慣”與性別有關,即精確的值應為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐![]() 的底面為矩形,D為
的底面為矩形,D為![]() 的中點,AC⊥平面BCC1B1.
的中點,AC⊥平面BCC1B1.

(Ⅰ)證明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的長;
(2)求B1D與平面ABB1所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的右焦點為
的右焦點為![]() ,右頂點為
,右頂點為![]() ,設離心率為
,設離心率為![]() ,且滿足
,且滿足![]() ,其中
,其中![]() 為坐標原點.
為坐標原點.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過點(0,1)的直線![]() 與橢圓交于
與橢圓交于![]() ,
,![]() 兩點,求
兩點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海州市六一兒童節(jié)期間在婦女兒童活動中心舉行小學生“海州杯”圍棋比賽,規(guī)則如下:甲、乙兩名選手比賽時,每局勝者得1分,負者得0分,比賽進行到有一人比對方多2分或賽滿6局時比賽結束.設某校選手甲與另一選手乙比賽時,甲每局獲勝的概率皆為![]() ,且各局比賽勝負互不影響,已知第二局比賽結束時比賽停止的概率為
,且各局比賽勝負互不影響,已知第二局比賽結束時比賽停止的概率為![]() .
.
(1)求![]() 的值;
的值;
(2)設![]() 表示比賽停止時已比賽的局數,求隨機變量
表示比賽停止時已比賽的局數,求隨機變量![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年時紅軍長征勝利80周年,某市電視臺舉辦紀念紅軍長征勝利80周年知識問答,宣傳長征精神.首先在甲、乙、丙、丁四個不同的公園進行支持簽名活動,其次在各公園簽名的人中按分層抽樣的方式抽取10名幸運之星,每人獲得一個紀念品,其數據表格如下:

(Ⅰ)求此活動中各公園幸運之星的人數;
(Ⅱ)從乙和丙公園的幸運之星中任選兩人接受電視臺記者的采訪,求這兩人均來自乙公園的概率;
(Ⅲ)電視臺記者對乙公園的簽名人進行了是否有興趣研究“紅軍長征”歷史的問卷調查,統(tǒng)計結果如下(單位:人):

據此判斷能否在犯錯誤的概率不超過0.01的前提下認為有興趣研究“紅軍長征”歷史與性別有關.
附臨界值表及公式:  ,其中
,其中![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,以上頂點和右焦點為直徑端點的圓與直線
,以上頂點和右焦點為直徑端點的圓與直線![]() 相切.
相切.
(1)求橢圓的標準方程;
(2)對于直線![]() 和點
和點![]() ,橢圓
,橢圓![]() 上是否存在不同的兩點
上是否存在不同的兩點![]() 與
與![]() 關于直線
關于直線![]() 對稱,且
對稱,且![]() ,若存在實數
,若存在實數![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校的一個社會實踐調查小組,在對該校學生的良好“用眼習慣”的調查中,隨機發(fā)放了120分問卷.對收回的100份有效問卷進行統(tǒng)計,得到如![]() 下列聯(lián)表:
下列聯(lián)表:
做不到科學用眼 | 能做到科學用眼 | 合計 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合計 | 75 | 25 | 100 |
(1)現按女生是否能做到科學用眼進行分層,從45份女生問卷中抽取了6份問卷,從這6份問卷中再隨機抽取3份,并記其中能做到科學用眼的問卷的份數![]() ,試求隨機變量
,試求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(2)若在犯錯誤的概率不超過![]() 的前提下認為良好“用眼習慣”與性別有關,那么根據臨界值表,最精確的
的前提下認為良好“用眼習慣”與性別有關,那么根據臨界值表,最精確的![]() 的值應為多少?請說明理由.
的值應為多少?請說明理由.
附:獨立性檢驗統(tǒng)計量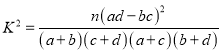 ,其中
,其中![]() .
.
獨立性檢驗臨界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com