
【題目】解關于![]() 的不等式
的不等式![]() .
.
【答案】當0<a<1時,解集為{x|x<1或x![]() };
};
當a=1時,解集為{x|x≠1};當a>1時,解集為{x|x![]() 或x>1}.
或x>1}.
【解析】
根據a大于1,a=1及a大于0小于1分三種情況取解集,當a大于1時,根據![]() 小于1,利用不等式取解集的方法求出解集;當a=1時,根據完全平方式大于0,得到x不等于1;當a大于0小于1時,根據
小于1,利用不等式取解集的方法求出解集;當a=1時,根據完全平方式大于0,得到x不等于1;當a大于0小于1時,根據![]() 大于1,利用不等式取解集的方法即可求出解集,綜上,寫出a不同取值時,各自的解集即可.
大于1,利用不等式取解集的方法即可求出解集,綜上,寫出a不同取值時,各自的解集即可.
由不等式得:![]()
(1)當![]() 時,
時,![]()
原不等式為:![]()
∴不等式的解集為:![]()
(2)當![]() 時,
時,![]()
原不等式為:![]()
![]()
∵![]()
∴不等式的解集為:{x|x<1或x![]() };
};
(3)當![]() 時,
時,![]()
原不等式為:![]()
![]()
∵![]() ,
,
∴不等式的解集為:{x|x![]() 或x>1},
或x>1},
綜上所述,得原不等式的解集為:
當0<a<1時,解集為{x|x<1或x![]() };
};
當a=1時,解集為{x|x≠1};當a>1時,解集為{x|x![]() 或x>1}.
或x>1}.


 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
: ![]() 的離心率是
的離心率是![]() ,且直線
,且直線![]() :
: ![]() 被橢圓
被橢圓![]() 截得的弦長為
截得的弦長為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若直線![]() 與圓
與圓![]() :
: ![]() 相切:
相切:
(i)求圓![]() 的標準方程;
的標準方程;
(ii)若直線![]() 過定點
過定點![]() ,與橢圓
,與橢圓![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() ,與圓
,與圓![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在空間直角坐標系Oxyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1, ![]() ),若S1 , S2 , S3分別表示三棱錐D﹣ABC在xOy,yOz,zOx坐標平面上的正投影圖形的面積,則( )
),若S1 , S2 , S3分別表示三棱錐D﹣ABC在xOy,yOz,zOx坐標平面上的正投影圖形的面積,則( )
A.S1=S2=S3
B.S2=S1且S2≠S3
C.S3=S1且S3≠S2
D.S3=S2且S3≠S1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形AMDE的邊長為2,B,C分別為AM,MD的中點,在五棱錐P﹣ABCDE中,F為棱PE的中點,平面ABF與棱PD,PC分別交于點G,H. 
(1)求證:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE,求直線BC與平面ABF所成角的大小,并求線段PH的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓的中心為原點O,長軸在x軸上,離心率 ![]() ,過左焦點F1作x軸的垂線交橢圓于A、A′兩點,|AA′|=4.
,過左焦點F1作x軸的垂線交橢圓于A、A′兩點,|AA′|=4. 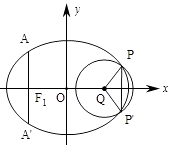
(1)求該橢圓的標準方程;
(2)取垂直于x軸的直線與橢圓相交于不同的兩點P、P′,過P、P′作圓心為Q的圓,使橢圓上的其余點均在圓Q外.若PQ⊥P'Q,求圓Q的標準方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com