
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
: ![]() 的離心率是
的離心率是![]() ,且直線
,且直線![]() :
: ![]() 被橢圓
被橢圓![]() 截得的弦長為
截得的弦長為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若直線![]() 與圓
與圓![]() :
: ![]() 相切:
相切:
(i)求圓![]() 的標準方程;
的標準方程;
(ii)若直線![]() 過定點
過定點![]() ,與橢圓
,與橢圓![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() ,與圓
,與圓![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(I)![]() ;(II)(i)
;(II)(i)![]() ;(ii)
;(ii)![]() .
.
【解析】試題分析:(Ⅰ)由直線![]() 過定點
過定點![]() ,
, ![]() ,可得到
,可得到![]() ,再結合
,再結合![]() ,即可求出橢圓的方程;(Ⅱ)(i)利用圓的幾何性質,求出圓心到直線
,即可求出橢圓的方程;(Ⅱ)(i)利用圓的幾何性質,求出圓心到直線![]() 的距離等于半徑,即可求出
的距離等于半徑,即可求出![]() 的值,即可求出圓
的值,即可求出圓![]() 的標準方程;(ii)首先設直線
的標準方程;(ii)首先設直線![]() 的方程為
的方程為![]() ,利用韋達定理即可求出弦長
,利用韋達定理即可求出弦長![]() 的表達式,同理利用圓的幾何關系可求出弦長
的表達式,同理利用圓的幾何關系可求出弦長![]() 的表達式,即可得到
的表達式,即可得到![]() 的表達式,再用換元法
的表達式,再用換元法![]() ,即可求出
,即可求出![]() 的取值范圍.
的取值范圍.
試題解析:
解:(Ⅰ)由已知得直線![]() 過定點
過定點![]() ,
, ![]() ,
, ![]() ,
,
又![]() ,
, ![]() ,解得
,解得![]() ,
, ![]() ,
,
故所求橢圓![]() 的標準方程為
的標準方程為![]() .
.
(Ⅱ)(i)由(Ⅰ)得直線![]() 的方程為
的方程為![]() ,即
,即![]() ,
,
又圓![]() 的標準方程為
的標準方程為![]() ,
,
∴圓心為![]() ,圓的半徑
,圓的半徑![]() ,
,
∴圓![]() 的標準方程為
的標準方程為![]() .
.
(ii)由題可得直線![]() 的斜率存在,
的斜率存在,
設![]() :
: ![]() ,與橢圓
,與橢圓![]() 的兩個交點為
的兩個交點為![]() 、
、![]() ,
,
由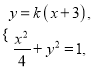 消去
消去![]() 得
得![]() ,
,
由![]() ,得
,得![]() ,
,
![]() ,
, ![]() ,
,
∴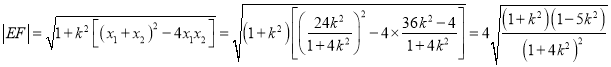 .
.
又圓![]() 的圓心
的圓心![]() 到直線
到直線![]() :
: ![]() 的距離
的距離![]() ,
,
∴圓![]() 截直線
截直線![]() 所得弦長
所得弦長![]() ,
,
∴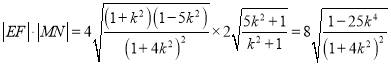 ,
,
設![]() ,
, ![]() ,
,
則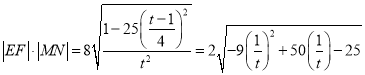 ,
,
∵![]() 的對稱軸為
的對稱軸為![]() ,在
,在![]() 上單調遞增,
上單調遞增, ![]() ,
,
∴![]() ,
,
∴![]() .
.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,已知acosB+bcosA=2ccosC.
(1)求角C的大小;
(2)若a=5,b=8,求邊c的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩家商場對同一種商品展開促銷活動,對購買該商品的顧客兩家商場的獎勵方案如下:
甲商場:顧客轉動如圖所示轉盤,當指針指向陰影部分(圖中兩個陰影部分均為扇形,且每個扇形圓心角均為![]() ,邊界忽略不計)即為中獎.
,邊界忽略不計)即為中獎.
乙商場:從裝有4個白球,4個紅球和4個籃球的盒子中一次性摸出3球(這些球初顏色外完全相同),如果摸到的是3個不同顏色的球,即為中獎.

(Ⅰ)試問:購買該商品的顧客在哪家商場中獎的可能性大?說明理由;
(Ⅱ)記在乙商場購買該商品的顧客摸到籃球的個數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中常數
,其中常數![]() .
.
(1)若![]() 在
在![]() 上單調遞增,求
上單調遞增,求![]() 的取值范圍;
的取值范圍;
(2)令![]() ,將函數
,將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位,再向上平移1個單位,得到函數
個單位,再向上平移1個單位,得到函數![]() 的圖象.區間
的圖象.區間![]() 滿足:
滿足:![]() 在
在![]() 上至少含有30個零點.在所有滿足上述條件的
上至少含有30個零點.在所有滿足上述條件的![]() 中,求
中,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD為正方形,平面PAD⊥平面ABCD,點M在線段PB上,PD∥平面MAC,PA=PD= ![]() ,AB=4.
,AB=4. 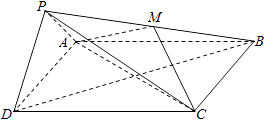
(1)求證:M為PB的中點;
(2)求二面角B﹣PD﹣A的大小;
(3)求直線MC與平面BDP所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com