Question

【題目】如圖，橢圓的中心為原點O，長軸在x軸上，離心率 ，過左焦點F1作x軸的垂線交橢圓于A、A′兩點，|AA′|=4．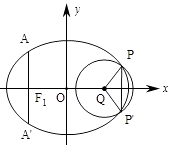

（1）求該橢圓的標準方程；
（2）取垂直于x軸的直線與橢圓相交于不同的兩點P、P′，過P、P′作圓心為Q的圓，使橢圓上的其余點均在圓Q外．若PQ⊥P'Q，求圓Q的標準方程．

Answer 1

【答案】
（1）解：由題意知點A（﹣c，2）在橢圓上，則 ，即 ①

∵離心率 ，∴ ②

聯立①②得： ，所以b2=8．

把b2=8代入②得，a2=16．

∴橢圓的標準方程為 ；

（2）解：設Q（t，0），圓Q的半徑為r，則圓Q的方程為（x﹣t）2+y2=r2，

不妨取P為第一象限的點，因為PQ⊥P'Q，則P（ ）（t＞0）．

聯立 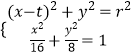，得x2﹣4tx+2t2+16﹣2r2=0．

由△=（﹣4t）2﹣4（2t2+16﹣2r2）=0，得t2+r2=8

又P（ ）在橢圓上，所以 ．

整理得， ．

代入t2+r2=8，得 ．

解得： ．所以 ， ．

此時 ．

滿足橢圓上的其余點均在圓Q外．

由對稱性可知，當t＜0時，t=﹣ ， ．

故所求圓Q的標準方程為

【解析】（1）利用點A（﹣c，2）在橢圓上，結合橢圓的離心率，求出幾何量，即可求得橢圓的標準方程；（2）設出圓Q的圓心坐標及半徑，由PQ⊥P'Q得到P的坐標，寫出圓的方程后和橢圓聯立，化為關于x的二次方程后由判別式等于0得到關于t與r的方程，把P點坐標代入橢圓方程得到關于t與r的另一方程，聯立可求出t與r的值，經驗證滿足橢圓上的其余點均在圓Q外，結合對稱性即可求得圓Q的標準方程．