
【題目】已知函數f(x)=lnx﹣ ![]() (a>0)
(a>0)
(1)若函數f(x)在x=2處的切線與x軸平行,求實數a的值;
(2)討論函數f(x)在區間[1,2]上的單調性;
(3)證明: ![]() >e.
>e.
【答案】
(1)解:∵ ![]() ,(x>0)
,(x>0)
∵函數f(x)在x=2處的切線與x軸平行
∴f′(2)= ![]() ,解得a=
,解得a= ![]()
(2)解:∵ ![]() =
= ![]() ,(x>0,a>0)
,(x>0,a>0)
令h(x)=ax2+(2a﹣2)x+a,(a>0),△=4﹣8a
①)當△=4﹣8a≤0,即a ![]() 時,f′(x)≥0在(0,+∞)恒成立,此時函數f(x)在區間[1,2]上單調遞增;
時,f′(x)≥0在(0,+∞)恒成立,此時函數f(x)在區間[1,2]上單調遞增;
②當△=4﹣8a>0,即0<a ![]() 時,拋物線y=ax2+(2a﹣2)x+a的圖象如下,與橫軸交點橫坐標為x1=
時,拋物線y=ax2+(2a﹣2)x+a的圖象如下,與橫軸交點橫坐標為x1= ![]() ,x2=
,x2= ![]()
h(1)=4a﹣2<0,h(2)=9a﹣4
當h(2)=9a﹣4≤0,即0 ![]() 時,h(x)≤0在(1,2)上恒成立,∴f′(x)≤0在(1,2)上恒成立,此時函數f(x)在區間[1,2]上單調遞減
時,h(x)≤0在(1,2)上恒成立,∴f′(x)≤0在(1,2)上恒成立,此時函數f(x)在區間[1,2]上單調遞減
當h(2)=9a﹣4<0,即 ![]() 時,h(x)≤0在(1,x2)上恒成立,h(x)≥0在(x2,2)上恒成立,此時函數f(x)在區間[1,
時,h(x)≤0在(1,x2)上恒成立,h(x)≥0在(x2,2)上恒成立,此時函數f(x)在區間[1, ![]() ]上單調遞減
]上單調遞減
,在( ![]() ,2)上單調遞增
,2)上單調遞增
(3)證明:由(2)可知,當a=0.5時,函數f(x)在區間[1,2]上單調遞增;即lnx ![]() 在區間[1,2]上恒成立.
在區間[1,2]上恒成立.
令x=1+ ![]() ,(n∈N+),則有ln(1+
,(n∈N+),則有ln(1+ ![]() )>
)> 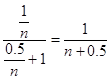
(n+0.5)ln ![]() >1ln(
>1ln( ![]() )n+0.5>1
)n+0.5>1 ![]() ,
,
令n=2017,可得 ![]() >e
>e
【解析】(1) ![]() ,(x>0)由f′(2)=
,(x>0)由f′(2)= ![]() ,解得a(2)
,解得a(2) ![]() =
= ![]() ,(x>0,a>0),令h(x)=ax2+(2a﹣2)x+a,(a>0),△=4﹣8a,分①)當△=4﹣8a≤0,即a
,(x>0,a>0),令h(x)=ax2+(2a﹣2)x+a,(a>0),△=4﹣8a,分①)當△=4﹣8a≤0,即a ![]() 時,②當△=4﹣8a>0,即0<a
時,②當△=4﹣8a>0,即0<a ![]() 討論;(3)由(2)可知,當a=0.5時,函數f(x)在區間[1,2]上單調遞增;即lnx
討論;(3)由(2)可知,當a=0.5時,函數f(x)在區間[1,2]上單調遞增;即lnx ![]() 在區間[1,2]上恒成立,令x=1+
在區間[1,2]上恒成立,令x=1+ ![]() ,(n∈N+),則有ln(1+
,(n∈N+),則有ln(1+ ![]() )>
)> 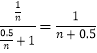 (n+0.5)ln
(n+0.5)ln ![]() >1ln(
>1ln( ![]() )n+0.5>1
)n+0.5>1 ![]() ,令n=2017,可得
,令n=2017,可得 ![]() >e.
>e.
【考點精析】利用利用導數研究函數的單調性對題目進行判斷即可得到答案,需要熟知一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減.
在這個區間單調遞減.


科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.極坐標系中方程ρ2﹣4ρcosθ=0和ρ﹣4cosθ=0表示的是同一曲線
B.![]()
C.不等式|a+b|≥|a|﹣|b|等號成立的條件為ab≤0
D.在極坐標系中方程 ![]() 表示的圓和一條直線.
表示的圓和一條直線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系 ![]() 中,曲線
中,曲線 ![]() 的方程為
的方程為 ![]() ,直線
,直線 ![]() 的傾斜角為
的傾斜角為 ![]() 且經過點
且經過點 ![]() .
.
(1)以 ![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,求曲線
軸的正半軸為極軸建立極坐標系,求曲線 ![]() 的極坐標方程;
的極坐標方程;
(2)設直線 ![]() 與曲線
與曲線 ![]() 交于兩點
交于兩點 ![]() ,
, ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() 的定義域為R
的定義域為R
(1)當a=2時,求函數f(x)的值域
(2)若函數f(x)是奇函數,①求a的值;②解不等式f(3﹣m)+f(3﹣m2)>0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經市場調查,某商品在過去的100天內的銷售量(單位:件)和價格(單位:元)均為時間![]() (單位:天)的函數,且銷售量滿足
(單位:天)的函數,且銷售量滿足![]() =
=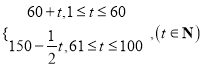 ,價格滿足
,價格滿足![]() =
=![]() .
.
(1)求該種商品的日銷售額![]() 與時間
與時間![]() 的函數關系;
的函數關系;
(2)若銷售額超過16610元,商家認為該商品的收益達到理想程度,請判斷該商品在哪幾天的收益達到理想程度?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個定點![]() ,動點
,動點![]() 滿足
滿足![]() .設動點
.設動點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() .
.
(1)求曲線![]() 的軌跡方程;
的軌跡方程;
(2)若![]() 與曲線
與曲線![]() 交于不同的
交于不同的![]() 兩點,且
兩點,且![]() (
(![]() 為坐標原點),求直線
為坐標原點),求直線![]() 的斜率;
的斜率;
(3)若![]() 是直線
是直線![]() 上的動點,過
上的動點,過![]() 作曲線
作曲線![]() 的兩條切線
的兩條切線![]() ,切點為
,切點為![]() ,探究:直線
,探究:直線![]() 是否過定點.
是否過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com