【題目】已知拋物線
，直線
、
（
），
與
恰有一個公共點
，
與恰有一個公共點
，與交于點
.
（1）當
時，求點到準線的距離；
（2）當與不垂直時，求
的取值范圍；
（3）設
是平面上一點，滿足
且
，求和的夾角大小.
科目：高中數學 來源： 題型：
【題目】港珠澳大橋是中國建設史上里程最長，投資最多，難度最大的跨海橋梁項目，大橋建設需要許多橋梁構件。從某企業生產的橋梁構件中抽取
件，測量這些橋梁構件的質量指標值，由測量結果得到如圖所示的頻率分布直方圖，質量指標值落在區間
，
，
內的頻率之比為
.
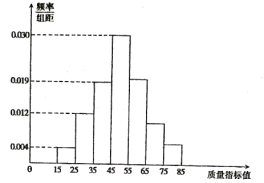
（1）求這些橋梁構件質量指標值落在區間內的頻率；
（2）用分層抽樣的方法在區間
內抽取一個容量為
的樣本，將該樣本看成一個總體，從中任意抽取
件橋梁構件，求這件橋梁構件都在區間
內的概率
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
，
為坐標原點，
為橢圓的左焦點，離心率為
，直線
與橢圓相交于
，
兩點.
（1）求橢圓的方程；
（2）若
是弦
的中點，
是橢圓上一點，求
的面積最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，且經過點
（1）求橢圓
的方程；
（2）是否存在經過點
的直線
，它與橢圓相交于
兩個不同點，且滿足
為坐標原點）關系的點
也在橢圓上，如果存在，求出直線的方程；如果不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】假設某種設備使用的年限
（年）與所支出的維修費用
（萬元）有以下統計資料：
使用年限 | 2 | 3 | 4 | 5 | 6 |
維修費用 | 2 | 4 | 5 | 6 | 7 |
若由資料知對呈線性相關關系.試求：
（1）求
；
（2）線性回歸方程
；
（3）估計使用10年時，維修費用是多少？
附：利用“最小二乘法”計算
的值時，可根據以下公式：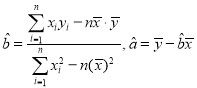
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
、
、
、
是同一平面上不共線的四點，若存在一組正實數
、
、
，使得
，則三個角
、
、
（ ）
A. 都是鈍角B. 至少有兩個鈍角
C. 恰有兩個鈍角D. 至多有兩個鈍角
查看答案和解析>>
科目：高中數學 來源： 題型：
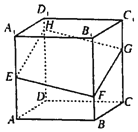
【題目】如圖，正方體
的棱長為
，作平面
與底面不平行
與棱
，
，
，
分別交于E，F，G，H，記EA，FB，GC，HD分別為
，
，
，
，若
，
，則多面體EFGHABCD的體積為
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
的參數方程為
（
為參數），以原點
為極點，
軸正半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（1）求曲線的普通方程及曲線的直角坐標方程，并指出兩曲線的軌跡圖形；
（2）曲線與兩坐標軸的交點分別為
、
，點
在曲線上運動，當曲線與曲線相切時，求
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
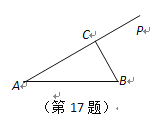
【題目】如圖所示，某公園內有兩條道路
，
，現計劃在上選擇一點
，新建道路
，并把
所在的區域改造成綠化區域．已知
，
．
（1）若綠化區域的面積為1
，求道路的長度；
（2）若綠化區域改造成本為10萬元/，新建道路成本為10萬元/．設
（
），當
為何值時，該計劃所需總費用最小？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
