
���}Ŀ����֪�E�A![]() ��
��![]() ��
��![]() ������(bi��o)ԭ�c(di��n)��
������(bi��o)ԭ�c(di��n)��![]() ��E�A
��E�A![]() �����c(di��n)���x���ʞ�
�����c(di��n)���x���ʞ�![]() ��ֱ��
��ֱ��![]() �c�E�A�ཻ��
�c�E�A�ཻ��![]() ��
��![]() ���c(di��n).
���c(di��n).
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2����![]() ����
����![]() �����c(di��n)��
�����c(di��n)��![]() �ǙE�A
�ǙE�A![]() ��һ�c(di��n)����
��һ�c(di��n)����![]() ����e���ֵ.
����e���ֵ.
���𰸡���1��![]() ����2��
����2��![]() .
.
��������
��1������(j��)![]() �����
�����![]() ���Y(ji��)���x���ʞ�
���Y(ji��)���x���ʞ�![]() �������
�������![]() ��
��![]() �����}�ý⡣
�����}�ý⡣
��2���O(sh��)![]() ��
��![]() .�O(sh��)ֱ��
.�O(sh��)ֱ��![]() �ķ��̞飺
�ķ��̞飺![]() ��(li��n)��ֱ���c�E�A���̿ɵã�
��(li��n)��ֱ���c�E�A���̿ɵã�![]() ���Y(ji��)��
���Y(ji��)��![]() �����
�����![]() ���������L(zh��ng)��ʽ���
���������L(zh��ng)��ʽ���![]() ��������ֱ���c�E�A��λ���P(gu��n)ϵ�������
��������ֱ���c�E�A��λ���P(gu��n)ϵ�������![]() �c(di��n)��ֱ��
�c(di��n)��ֱ��![]() �ľ��x�����ֵ�����}�ý⡣
�ľ��x�����ֵ�����}�ý⡣
�⣺��![]() ��
��![]() ��E�A
��E�A![]() �����c(di��n)��
�����c(di��n)��
�O(sh��)�E�A![]() �Ľ�����
�Ľ�����![]() ������
������![]() ��
��
���x���ʞ�![]() ����
����![]() ����
����![]() ������
������![]() ��
��
���E�A![]() �ķ��̞飺
�ķ��̞飺![]() .
.
��2���O(sh��)![]() ��
��![]() .
.
��![]() ����
����![]() �����c(di��n)����ֱ��
�����c(di��n)����ֱ��![]() ��б�ʴ��ڣ��O(sh��)б�ʞ�
��б�ʴ��ڣ��O(sh��)б�ʞ�![]() ��
��
�tֱ��![]() �ķ��̞飺
�ķ��̞飺![]() ����
����![]() .
.
��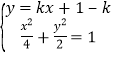 (li��n)���������ã�
(li��n)���������ã�![]() ��
��
��?y��n)�ֱ���c�E�A�ཻ������![]() ����.
����.
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��ֱ��![]() �ķ��̞飺
�ķ��̞飺![]() ��
��![]() ��
��![]() ��
��
��![]()
![]() .
.
Ҫʹ![]() ����e���ֵ����
����e���ֵ����![]() �Ƕ�ֵ����
�Ƕ�ֵ����![]() �c(di��n)��
�c(di��n)��![]() �ľ��x���.
�ľ��x���.
�O(sh��)�cֱ��![]() ƽ�е�ֱ�����̞飺
ƽ�е�ֱ�����̞飺![]() ��
��
�ɷ��̽M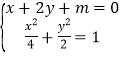 (li��n)������
(li��n)������![]() ��
��
��![]() ����
����![]() .
.
��![]() �ǙE�A
�ǙE�A![]() ��һ�c(di��n)��
��һ�c(di��n)��
��![]() �c(di��n)��
�c(di��n)��![]() �������x����ֱ��
�������x����ֱ��![]() ��ֱ��
��ֱ��![]() �ľ��x
�ľ��x![]() .
.
��![]() ��
��
�˕r(sh��)![]()
![]() .
.
��ˣ�![]() ����e���ֵ��
����e���ֵ��![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���x��4-5������ʽ�x�v
��֪����(sh��)![]() .
.
���ⲻ��ʽ�� ![]() ��
��
����(d��ng)![]() �r(sh��)������(sh��)
�r(sh��)������(sh��)![]() �ĈD���c
�ĈD���c![]() �S����һ��(g��)�����Σ���(sh��)��(sh��)
�S����һ��(g��)�����Σ���(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����֪�c(di��n)C�LjA�Ğ�O�돽��1�İ�A���Ϗ��c(di��n)A��(sh��)��ĵ�һ��(g��)���ȷ��c(di��n)��![]() ��ֱ����
��ֱ����![]() ��ֱ��
��ֱ��![]() ƽ��
ƽ��![]() .
.
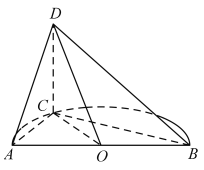
��1���C����![]() ��
��
��2����M��![]() �����c(di��n)�����C��
�����c(di��n)�����C��![]() ƽ��
ƽ��![]() ��
��
��3���������F![]() ���w�e.
���w�e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ڢ�![]() ;��
;��![]() �@�ɂ�(g��)�l�������x-һ��(g��)���a(b��)�������憖�}�У�Ȼ�����a(b��)���������}.
�@�ɂ�(g��)�l�������x-һ��(g��)���a(b��)�������憖�}�У�Ȼ�����a(b��)���������}.

��![]() ����
�У���![]() �Č�(du��)߅�քe��
�Č�(du��)߅�քe��![]() ����֪ ��
����֪ ��![]() .
.
(1)��![]() ;
;
(2)��D��![]() ��߅
��߅![]() ��һ�c(di��n)��
��һ�c(di��n)��![]() ����
����![]() ����e
����e
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
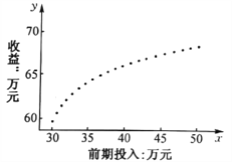
���}Ŀ��ij��(li��n)�W(w��ng)��˾���˴_����һ���ȵ�ǰ�ڏV��Ͷ��Ӌ(j��)�����ռ��˽���ǰ�ڏV��Ͷ����![]() ����λ���fԪ��������
����λ���fԪ��������![]() ����λ���fԪ���Ĕ�(sh��)��(j��)����(du��)�@Щ��(sh��)��(j��)���˳���̎�����õ��������ɢ�c(di��n)�D����
����λ���fԪ���Ĕ�(sh��)��(j��)����(du��)�@Щ��(sh��)��(j��)���˳���̎�����õ��������ɢ�c(di��n)�D����![]() ��(g��)��(sh��)��(j��)�c(di��n)����һЩ�y(t��ng)Ӌ(j��)����ֵ.�����M(j��n)һ���˽�V��Ͷ����
��(g��)��(sh��)��(j��)�c(di��n)����һЩ�y(t��ng)Ӌ(j��)����ֵ.�����M(j��n)һ���˽�V��Ͷ����![]() ��(du��)����
��(du��)����![]() ��Ӱ푣���˾��λ�T���٢ڢی�(du��)�vʷ��(sh��)��(j��)�M(j��n)�з�������醴����Y�ϣ��քe���������(g��)�ؚw����ģ�ͣ�
��Ӱ푣���˾��λ�T���٢ڢی�(du��)�vʷ��(sh��)��(j��)�M(j��n)�з�������醴����Y�ϣ��քe���������(g��)�ؚw����ģ�ͣ�
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
����(j��)![]() ��
�� ![]() ��������(sh��)��(j��)��
��������(sh��)��(j��)�� ![]() ��
�� ![]() .
.
��1������(j��)ɢ�c(di��n)�D�Д࣬��һλ�T�������ģ�Ͳ��m���Á�����![]() �c
�c![]() ֮�g���P(gu��n)ϵ����(ji��n)Ҫ�f������.
֮�g���P(gu��n)ϵ����(ji��n)Ҫ�f������.
��2������(j��)��1�����Д�Y(ji��)�������Д�(sh��)��(j��)�������ɂ�(g��)ģ���зքe��������![]() �P(gu��n)��Ͷ����
�P(gu��n)��Ͷ����![]() ���P(gu��n)ϵ�����Ĕ�(sh��)��(j��)���P(gu��n)�ԵĽǶȿ��]��������λ�T������Ļؚwģ���У���һ��(g��)���(y��u)ģ�ͣ������m����������
���P(gu��n)ϵ�����Ĕ�(sh��)��(j��)���P(gu��n)�ԵĽǶȿ��]��������λ�T������Ļؚwģ���У���һ��(g��)���(y��u)ģ�ͣ������m����������![]() �Ļؚw���̣����f�����ɣ�
�Ļؚw���̣����f�����ɣ�
������(du��)��һ�M��(sh��)��(j��)![]() ��
�� ![]() ������
������ ![]() ����ؚwֱ��
����ؚwֱ��![]() ��б�ʡ��ؾ����С���˹�Ӌ(j��)�Լ����P(gu��n)ϵ��(sh��)�քe�飺
��б�ʡ��ؾ����С���˹�Ӌ(j��)�Լ����P(gu��n)ϵ��(sh��)�քe�飺
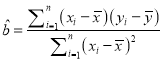 ��
�� ![]() ��
�� 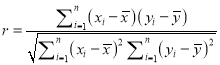 ��
��
����![]() Խ�ӽ���
Խ�ӽ���![]() ���f��׃��
���f��׃��![]() �c
�c![]() �ľ������P(gu��n)�̶�Խ��.
�ľ������P(gu��n)�̶�Խ��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�AC��![]() ���x���ʞ�
���x���ʞ�![]() ���L(zh��ng)���S�L(zh��ng)����S�L(zh��ng)��b����A��B�քe��E�AC���ϡ�����c(di��n)���c(di��n)
���L(zh��ng)���S�L(zh��ng)����S�L(zh��ng)��b����A��B�քe��E�AC���ϡ�����c(di��n)���c(di��n)![]() ��
��
![]() ��E�AC�ķ��̣�
��E�AC�ķ��̣�
![]() ��ֱ��MA��MB�c�E�AC����һ���c(di��n)�քe��P��Q���C����ֱ��PQ�^���c(di��n)��
��ֱ��MA��MB�c�E�AC����һ���c(di��n)�քe��P��Q���C����ֱ��PQ�^���c(di��n)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ֱ֪��![]() �^�c(di��n)
�^�c(di��n)![]() ���A
���A![]() ��
��![]() .
.
��1����(d��ng)ֱ��![]() �c�A���Еr(sh��)����ֱ��
�c�A���Еr(sh��)����ֱ��![]() ��һ�㷽�̣�
��һ�㷽�̣�
��2����ֱ���c�A�ཻ�������L(zh��ng)��![]() ����ֱ��
����ֱ��![]() ��һ�㷽��.
��һ�㷽��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ڿո��(n��i)���롰��ַDZ�Ҫ����Ҫ�dz�֡���Ҫ���ȷdz���ַDZ�Ҫ��.
��1����![]() ���ǡ�
���ǡ�![]() ����________�l����
����________�l����
��2����![]() ���ǡ�
���ǡ�![]() ����________�l����
����________�l����
��3����֪![]() ��
��![]() ����
����![]() ���ǡ�
���ǡ�![]() ����________�l����
����________�l����
��4����![]() ���ǡ�
���ǡ�![]() ����________�l����
����________�l����
��5����![]() ���ǡ�AB����________�l����
���ǡ�AB����________�l����
��6����![]() ���ǡ�
���ǡ�![]() ����________�l����
����________�l����
��7��������AB���ǡ�![]() ����________�l����
����________�l����
��8����֪![]() ����
����![]() ���ǡ�
���ǡ�![]() ����________�l��.
����________�l��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������к���(sh��)��ֵ��͆��{(di��o)�^(q��)�g��
��1��![]() ��
��
��2��![]() .
.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com