
【題目】已知曲線![]() 的焦點(diǎn)是
的焦點(diǎn)是![]() ,
,![]() 、
、![]() 是曲線
是曲線![]() 上不同兩點(diǎn),且存在實(shí)數(shù)
上不同兩點(diǎn),且存在實(shí)數(shù)![]() 使得
使得![]() ,曲線
,曲線![]() 在點(diǎn)
在點(diǎn)![]() 、
、![]() 處的兩條切線相交于點(diǎn)
處的兩條切線相交于點(diǎn)![]() .
.
(1)求點(diǎn)![]() 的軌跡方程;
的軌跡方程;
(2)點(diǎn)![]() 在
在![]() 軸上,以
軸上,以![]() 為直徑的圓與
為直徑的圓與![]() 的另一交點(diǎn)恰好是
的另一交點(diǎn)恰好是![]() 的中點(diǎn),當(dāng)
的中點(diǎn),當(dāng)![]() 時(shí),求四邊形
時(shí),求四邊形![]() 的面積.
的面積.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由題意知![]() 、
、![]() 、
、![]() 三點(diǎn)共線,可設(shè)直線
三點(diǎn)共線,可設(shè)直線![]() 的方程為
的方程為![]() ,并設(shè)點(diǎn)
,并設(shè)點(diǎn)![]() ,
,![]() ,將直線
,將直線![]() 的方程與曲線
的方程與曲線![]() 的方程聯(lián)立,并列出韋達(dá)定理,利用導(dǎo)數(shù)求出曲線
的方程聯(lián)立,并列出韋達(dá)定理,利用導(dǎo)數(shù)求出曲線![]() 在點(diǎn)
在點(diǎn)![]() 、
、![]() 處的切線方程,將兩切線方程聯(lián)立,求出點(diǎn)
處的切線方程,將兩切線方程聯(lián)立,求出點(diǎn)![]() 的坐標(biāo),即可得出點(diǎn)
的坐標(biāo),即可得出點(diǎn)![]() 的軌跡方程;
的軌跡方程;
(2)由![]() ,利用坐標(biāo)運(yùn)算得出
,利用坐標(biāo)運(yùn)算得出![]() ,代入韋達(dá)定理解出
,代入韋達(dá)定理解出![]() ,根據(jù)對稱性取
,根據(jù)對稱性取![]() ,求出線段
,求出線段![]() 的中點(diǎn)
的中點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為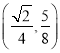 ,由
,由![]() 轉(zhuǎn)化為
轉(zhuǎn)化為![]() 可求出點(diǎn)
可求出點(diǎn)![]() 的坐標(biāo),并得出點(diǎn)
的坐標(biāo),并得出點(diǎn)![]() 的坐標(biāo),利用弦長公式計(jì)算出
的坐標(biāo),利用弦長公式計(jì)算出![]() ,利用點(diǎn)到直線的距離公式分別計(jì)算出
,利用點(diǎn)到直線的距離公式分別計(jì)算出![]() 和
和![]() 的高,并計(jì)算出這兩個(gè)三角形的面積,相加即可得出四邊形
的高,并計(jì)算出這兩個(gè)三角形的面積,相加即可得出四邊形![]() 的面積.
的面積.
(1)曲線![]() 就是拋物線
就是拋物線![]() ,它的焦點(diǎn)坐標(biāo)為
,它的焦點(diǎn)坐標(biāo)為![]() .
.
存在實(shí)數(shù)![]() 使得
使得![]() ,則
,則![]() 、
、![]() 、
、![]() 三點(diǎn)共線.
三點(diǎn)共線.
當(dāng)直線斜率不存在時(shí),不符合題意;
當(dāng)直線![]() 的斜率存在時(shí),設(shè)直線
的斜率存在時(shí),設(shè)直線![]() 的方程為
的方程為![]() ,與
,與![]() 聯(lián)立消去
聯(lián)立消去![]() ,整理得
,整理得![]() ,判別式
,判別式![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,
則![]() 、
、![]() 就是方程
就是方程![]() 的兩實(shí)根,
的兩實(shí)根,![]() ,
,![]() .
.
![]() ,
,![]() ,切線斜率
,切線斜率![]() ,
,
則曲線![]() 在點(diǎn)
在點(diǎn) 處的切線方程是
處的切線方程是![]() ,即
,即![]() ①.
①.
同理得曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程是
處的切線方程是![]() ②.
②.
聯(lián)立①②得 ,得
,得 ,所以點(diǎn)
,所以點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
因此,點(diǎn)![]() 的軌跡方程為
的軌跡方程為![]() ;
;
(2)已知![]() ,在(1)的解答的基礎(chǔ)上,
,在(1)的解答的基礎(chǔ)上,
![]() ,
,![]() ,則
,則![]() ,
,![]() .
.
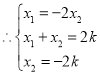 ,解得
,解得![]() ,
,![]() ,代入
,代入![]() 中,解得
中,解得![]() ,
,
注意到對稱性,求四邊形![]() 面積,只需取
面積,只需取![]() 即可.
即可.
![]() ,設(shè)
,設(shè)![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,則
,則![]() ,
,![]() .
.
已知點(diǎn)![]() 在以點(diǎn)
在以點(diǎn)![]() 為直徑的圓上,則
為直徑的圓上,則![]() ,
,
設(shè)![]() ,由
,由![]() ,得
,得![]() ,即
,即 ,
,
解得![]() ,則
,則![]() .
.
將直線![]() 的方程
的方程![]() 化為
化為![]() ,
,
則點(diǎn)![]() 到
到![]() 的距離
的距離 .
.
所以![]() .
.
在(1)的解答中,聯(lián)立①②消去![]() 解得
解得![]() ,
,
則兩切線交點(diǎn)坐標(biāo)為![]() ,
,
![]() 時(shí),
時(shí),![]() ,此時(shí),點(diǎn)
,此時(shí),點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為 .
.
![]() 到
到![]() 的距離
的距離 .
.
所以![]() .
.
又已知![]() 、
、![]() 在
在![]() 兩側(cè),所以
兩側(cè),所以![]() .
.


 培優(yōu)好卷單元加期末卷系列答案
培優(yōu)好卷單元加期末卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)![]()
(1)求![]() 的值;
的值;
(2)![]() 時(shí),求
時(shí),求![]() 的取值范圍;
的取值范圍;
(3)函數(shù)的性質(zhì)通常指的是函數(shù)的定義域、值域、單調(diào)性、周期性、奇偶性等,請你探究函數(shù)![]() 其中的三個(gè)性質(zhì)(直接寫出結(jié)論即可)
其中的三個(gè)性質(zhì)(直接寫出結(jié)論即可)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為考察某種藥物預(yù)防疾病的效果,進(jìn)行動物試驗(yàn),調(diào)查了 105 個(gè)樣本,統(tǒng)計(jì)結(jié)果為:服藥的共有 55 個(gè)樣本,服藥但患病的仍有 10 個(gè)樣本,沒有服藥且未患病的有 30個(gè)樣本.
(1)根據(jù)所給樣本數(shù)據(jù)完成 ![]() 列聯(lián)表中的數(shù)據(jù);
列聯(lián)表中的數(shù)據(jù);
(2)請問能有多大把握認(rèn)為藥物有效?
(參考公式:![]() 獨(dú)立性檢驗(yàn)臨界值表
獨(dú)立性檢驗(yàn)臨界值表
概率 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
患病 | 不患病 | 合計(jì) | |
服藥 | |||
沒服藥 | |||
合計(jì) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,
,![]() ,直線
,直線![]() (
(![]() )與橢圓
)與橢圓![]() 交于
交于![]() ,
,![]() 兩點(diǎn)(點(diǎn)
兩點(diǎn)(點(diǎn)![]() 在
在![]() 軸的上方).
軸的上方).
(1)若![]() ,求
,求![]() 的面積;
的面積;
(2)是否存在實(shí)數(shù)![]() 使得以線段
使得以線段![]() 為直徑的圓恰好經(jīng)過坐標(biāo)原點(diǎn)
為直徑的圓恰好經(jīng)過坐標(biāo)原點(diǎn)![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在![]() 中,
中,![]() 分別為內(nèi)角
分別為內(nèi)角![]() 所對的邊,且滿足
所對的邊,且滿足![]() .
.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)現(xiàn)給出三個(gè)條件:①![]() ; ②
; ②![]() ;③
;③![]() .
.
試從中選出兩個(gè)可以確定![]() 的條件,寫出你的選擇并以此為依據(jù)求
的條件,寫出你的選擇并以此為依據(jù)求![]() 的面積 (只需寫出一個(gè)選定方案即可,選多種方案以第一種方案記分)
的面積 (只需寫出一個(gè)選定方案即可,選多種方案以第一種方案記分)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,則下列命題正確的是______
,則下列命題正確的是______![]() 填上你認(rèn)為正確的所有命題的序號
填上你認(rèn)為正確的所有命題的序號![]()
![]() 函數(shù)
函數(shù)![]() 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是![]() ;
;![]() 函數(shù)
函數(shù)![]() 的圖像關(guān)于點(diǎn)
的圖像關(guān)于點(diǎn)![]() 對稱;
對稱;
![]() 函數(shù)
函數(shù)![]() 的圖像向左平移
的圖像向左平移![]() 個(gè)單位長度后,所得的圖像關(guān)于y軸對稱,則m的最小值是
個(gè)單位長度后,所得的圖像關(guān)于y軸對稱,則m的最小值是![]() ;
;
![]() 若實(shí)數(shù)m使得方程
若實(shí)數(shù)m使得方程![]() 在
在![]() 上恰好有三個(gè)實(shí)數(shù)解
上恰好有三個(gè)實(shí)數(shù)解![]() ,
,![]() ,
,![]() ,則
,則![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,以原點(diǎn)O為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,直線L:![]() ,曲線C的參數(shù)方程為
,曲線C的參數(shù)方程為![]() (
(![]() 為參數(shù))
為參數(shù))
![]() 求直線L和曲線C的普通方程;
求直線L和曲線C的普通方程;
![]() 在曲線C上求一點(diǎn)Q,使得Q到直線L的距離最小,并求出這個(gè)最小值
在曲線C上求一點(diǎn)Q,使得Q到直線L的距離最小,并求出這個(gè)最小值![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】橢圓![]() 經(jīng)過
經(jīng)過![]() 為坐標(biāo)原點(diǎn),線段
為坐標(biāo)原點(diǎn),線段![]() 的中點(diǎn)在圓
的中點(diǎn)在圓![]() 上.
上.
(1)求![]() 的方程;
的方程;
(2)直線![]() 不過曲線
不過曲線![]() 的右焦點(diǎn)
的右焦點(diǎn)![]() ,與
,與![]() 交于
交于![]() 兩點(diǎn),且
兩點(diǎn),且![]() 與圓
與圓![]() 相切,切點(diǎn)在第一象限,
相切,切點(diǎn)在第一象限, ![]() 的周長是否為定值?并說明理由.
的周長是否為定值?并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地區(qū)實(shí)施“光盤行動”以后,某自助啤酒吧也制定了自己的行動計(jì)劃,進(jìn)店的每一位客人需預(yù)交![]() 元,啤酒根據(jù)需要自己用量杯量取,結(jié)賬時(shí),根據(jù)每桌剩余酒量,按一定倍率收費(fèi)(如下表),每桌剩余酒量不足
元,啤酒根據(jù)需要自己用量杯量取,結(jié)賬時(shí),根據(jù)每桌剩余酒量,按一定倍率收費(fèi)(如下表),每桌剩余酒量不足![]() 升的,按
升的,按![]() 升計(jì)算(如剩余
升計(jì)算(如剩余![]() 升,記為剩余
升,記為剩余![]() 升).例如:結(jié)賬時(shí),某桌剩余酒量恰好為
升).例如:結(jié)賬時(shí),某桌剩余酒量恰好為![]() 升,則該桌的每位客人還應(yīng)付
升,則該桌的每位客人還應(yīng)付![]() 元.統(tǒng)計(jì)表明飲酒量與人數(shù)有很強(qiáng)的線性相關(guān)關(guān)系,下面是隨機(jī)采集的
元.統(tǒng)計(jì)表明飲酒量與人數(shù)有很強(qiáng)的線性相關(guān)關(guān)系,下面是隨機(jī)采集的![]() 組數(shù)據(jù)
組數(shù)據(jù)![]() (其中
(其中![]() 表示飲酒人數(shù),
表示飲酒人數(shù),![]() (升)表示飲酒量):
(升)表示飲酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
剩余酒量(單位:升) |
|
|
|
|
|
結(jié)賬時(shí)的倍率 |
|
|
|
|
|
(1)求由這![]() 組數(shù)據(jù)得到的
組數(shù)據(jù)得到的![]() 關(guān)于
關(guān)于![]() 的回歸直線方程;
的回歸直線方程;
(2)小王約了![]() 位朋友坐在一桌飲酒,小王及朋友用量杯共量取了
位朋友坐在一桌飲酒,小王及朋友用量杯共量取了![]() 升啤酒,這時(shí),酒吧服務(wù)生對小王說,根據(jù)他的經(jīng)驗(yàn),小王和朋友量取的啤酒可能喝不完,可以考慮再邀請
升啤酒,這時(shí),酒吧服務(wù)生對小王說,根據(jù)他的經(jīng)驗(yàn),小王和朋友量取的啤酒可能喝不完,可以考慮再邀請![]() 位或
位或![]() 位朋友一起來飲酒,會更劃算.試向小王是否該接受服務(wù)生的建議?
位朋友一起來飲酒,會更劃算.試向小王是否該接受服務(wù)生的建議?
參考數(shù)據(jù):回歸直線的方程是![]() ,其中
,其中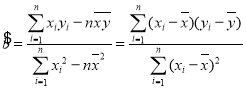 ,
,![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com