
【題目】提高過江大橋的車輛通行能力可改善整個城市的交通狀況.在一般情況下,大橋上的車流速度v(單位:千米/小時)是車流密度x(單位:輛/千米)的函數.當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時.研究表明:當![]() 時,車流速度
時,車流速度![]() 是車流密度
是車流密度![]() 的一次函數.
的一次函數.
(1)當![]() 時,求函數
時,求函數![]() 的表達式;
的表達式;
(2)當車流密度![]() 為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)
為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)![]() 可以達到最大,并求出最大值.(精確到1輛/小時)
可以達到最大,并求出最大值.(精確到1輛/小時)
【答案】(1)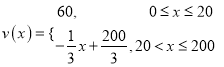 ;
;
(2)當車流密度為![]() 輛/千米時,車流量達到最大,且最大值約
輛/千米時,車流量達到最大,且最大值約![]() 輛/小時.
輛/小時.
【解析】試題分析:(1)設v(x)=ax+b.利用x的范圍,列出方程組求解a,b,即可得到函數的解析式;(2)求出車流量f(x)=v(x)x的表達式,然后求解最大值即可
試題解析:(1)由題意:當0≤x≤20時,v(x)=60;
當20≤x≤200時,設v(x)=ax+b,
再由已知得![]() 解得
解得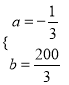 故函數v(x)的表達式為
故函數v(x)的表達式為
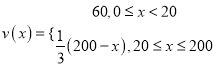
(2)依題意并由(1)可得
f(x)=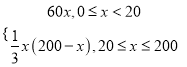
當0≤x≤20時,f(x)為增函數,故當x=20時,其最大值為60×20=1200;
當20≤x≤200時,f(x)=![]() x(200-x)≤
x(200-x)≤![]() [
[![]() ]2=
]2=![]() ,
,
當且僅當x=200-x,即x=100時,等號成立.
所以,當x=100時,f(x)在區間上取得最大值![]() .
.
綜上,當x=100時,f(x)在區間上取得最大值![]() ≈3 333,
≈3 333,
即當車流密度為100輛/千米時,車流量可以達到最大,最大值約為3 333輛/小時.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() x3﹣
x3﹣ ![]() (a∈R).
(a∈R).
(1)若a=1,求函數f(x)在[0,2]上的最大值;
(2)若對任意x∈(0,+∞),有f(x)>0恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電視傳媒公司為了解某地區電視觀眾對里約奧運會的收視情況,隨機抽取了100名觀眾進行調查,其中女性有55名,下面是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖:
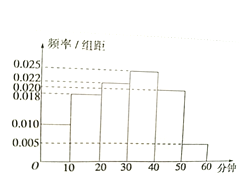
將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”。已知“體育迷”中有10名女性。
(1)試求“體育迷”中的男性觀眾人數;
(2)據此資料完成![]() 列聯表,你是否認為“體育迷”與性別有關?
列聯表,你是否認為“體育迷”與性別有關?
非體育迷 | 體育迷 | 合計 | |
男 | |||
女 | |||
合計 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
臨界值表供參考參考公式:
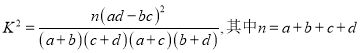
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若橢圓C1: ![]() 的離心率等于
的離心率等于 ![]() ,拋物線C2:x2=2py(p>0)的焦點在橢圓C1的頂點上.
,拋物線C2:x2=2py(p>0)的焦點在橢圓C1的頂點上.
(1)求拋物線C2的方程;
(2)求過點M(﹣1,0)的直線l與拋物線C2交E、F兩點,又過E、F作拋物線C2的切線l1、l2 , 當l1⊥l2時,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于三次函數f(x)=ax3+bx2+cx+d(a≠0),給出定義:設f′(x)是函數y=f(x)的導數,f′′(x)是f′(x)的導數,若方程f′′(x)有實數解x0 , 則稱點(x0 , f(x0))為函數y=f(x)的“拐點”.某同學經過探究發現:任何一個三次函數都有“拐點”;任何一個三次函數都有對稱中心,且“拐點”就是對稱中心.設函數f(x)= ![]() x3﹣
x3﹣ ![]() x2+3x﹣
x2+3x﹣ ![]() ,請你根據這一發現,計算f(
,請你根據這一發現,計算f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )= .
)= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log4(4x+1)﹣ ![]() x.
x.
(1)試判斷函數f(x)的奇偶性并證明;
(2)設g(x)=log4(a2x﹣ ![]() a),若函數f(x)與g(x)的圖象有且只有一個公共點,求實數a的取值范圍.
a),若函數f(x)與g(x)的圖象有且只有一個公共點,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com