【題目】現有一副斜邊長為10的直角三角板，將它們斜邊
重合，若將其中一個三角板沿斜邊折起形成三棱錐
，如圖所示，已知
，
，則三棱錐的外接球的表面積為______；該三棱錐體積的最大值為_______．
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，直線l的參數方程為
（t為參數），曲線C的參數方程為
（θ為參數）.
（1）當
時，求直線l與曲線C的普通方程；
（2）若直線l與曲線C交于A，B兩點，直線l傾斜角的范圍為（0，
]，且P點的直角坐標為（0，2），求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的右焦點為F，直線l與C交于M，N兩點.
（1）若l過點F，點M，N到直線y＝2的距離分別為d1，d2，且
，求l的方程；
（2）若點M的坐標為（0，1），直線m過點M交C于另一點N′，當直線l與m的斜率之和為2時，證明：直線NN′過定點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】近年來，共享單車在我國各城市迅猛發展，為人們的出行提供了便利，但也給城市的交通管理帶來了一些困難，為掌握共享單車在
省的發展情況，某調查機構從該省抽取了5個城市，并統計了共享單車的
指標
和
指標
，數據如下表所示：
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
（1）試求與間的相關系數
，并說明與是否具有較強的線性相關關系（若
，則認為與具有較強的線性相關關系，否則認為沒有較強的線性相關關系）.
（2）建立關于的回歸方程，并預測當指標為7時，指標的估計值.
（3）若某城市的共享單車指標在區間
的右側，則認為該城市共享單車數量過多，對城市的交通管理有較大的影響交通管理部門將進行治理，直至指標在區間內現已知省某城市共享單車的指標為13，則該城市的交通管理部門是否需要進行治理？試說明理由.
參考公式：回歸直線
中斜率和截距的最小二乘估計分別為
，，
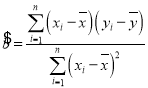相關系數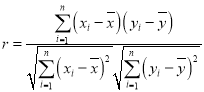
參考數據：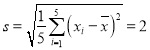
，
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，在直角梯形
中，
，
、
分別是
、
上的點，
，且
（如圖①）.將四邊形
沿
折起，連接
、、（如圖②）.在折起的過程中，則下列表述：
①
平面
；
②四點
、
、
、
可能共面；
③若
，則平面
平面
；
④平面
與平面可能垂直.其中正確的是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
