
【題目】已知三棱柱![]() 中,
中,![]() 、
、![]() 分別是
分別是![]() 與
與![]() 的中點(diǎn),
的中點(diǎn),![]() 為等邊三角形,
為等邊三角形,![]() ,
,![]() .
.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)(i)求證:![]() 平面
平面![]() ;
;
(ii)求二面角![]() 的正弦值.
的正弦值.
【答案】(Ⅰ)見(jiàn)解析(Ⅱ)(i)見(jiàn)解析(ii)![]()
【解析】
(Ⅰ)由![]() 推出
推出![]() 平面
平面![]() ,由
,由![]() 推出
推出![]() 平面
平面![]() ,則平面
,則平面![]() 平面
平面![]() ,由
,由![]() 平面PMN即可得證;(Ⅱ)(i)勾股定理證明
平面PMN即可得證;(Ⅱ)(i)勾股定理證明![]() 、
、![]() ,即可推出
,即可推出![]() 平面
平面![]() ;(ii)建立空間直角坐標(biāo)系,求出平面AMN,平面BMN的法向量代入
;(ii)建立空間直角坐標(biāo)系,求出平面AMN,平面BMN的法向量代入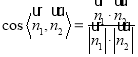 即可求得兩向量夾角的余弦值,再求出正弦值即可.
即可求得兩向量夾角的余弦值,再求出正弦值即可.
(Ⅰ)取![]() 中點(diǎn)
中點(diǎn)![]() ,連接MP,則
,連接MP,則![]() ,
,
因?yàn)?/span>![]() 平面ABC,
平面ABC,![]() 平面ABC,所以
平面ABC,所以![]() 平面
平面![]() ,
,
因?yàn)?/span>N、P分別![]() 的中點(diǎn),所以
的中點(diǎn),所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
因?yàn)?/span>![]() 平面ABC,
平面ABC,![]() 平面ABC,故
平面ABC,故![]() 平面
平面![]() ,
,
因?yàn)?/span>![]() ,
,![]() 平面PMN,
平面PMN,![]() 平面PMN,
平面PMN,
于是平面![]() 平面
平面![]() ,
,
又![]() 平面PMN,所以
平面PMN,所以![]() 平面
平面![]() .
.
(Ⅱ)(i)不妨設(shè)![]() ,則
,則![]() .
.
依題意![]() ,故
,故![]() 為等腰
為等腰![]() 底邊上的中線(xiàn),則
底邊上的中線(xiàn),則![]() .
.
于是![]() ,
,
因?yàn)?/span>![]() ,所以
,所以![]() ,同理
,同理![]() ,則
,則![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(ii)方法一:因?yàn)?/span>![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
因?yàn)?/span>![]() 為等邊三角形且
為等邊三角形且![]() 為
為![]() 的中點(diǎn),所以
的中點(diǎn),所以![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() 平面AMN,故平面
平面AMN,故平面![]() 平面
平面![]() .
.
設(shè)![]() ,則
,則![]() 為平面
為平面![]() 與平面
與平面![]() 的交線(xiàn).過(guò)
的交線(xiàn).過(guò)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,則
,則![]() 平面
平面![]() .又過(guò)
.又過(guò)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,則
,則![]() 平面
平面![]() ,
,![]() 即為二面角
即為二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,![]() ,則
,則![]() ;
;
在![]() 中,
中,![]() .
.
所以![]() ,即二面角
,即二面角![]() 的正弦值是
的正弦值是![]() .
.
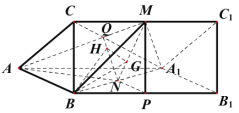
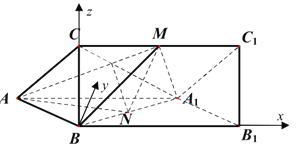
方法二:以![]() 為原點(diǎn),建立如圖所示的空間直角坐標(biāo)系.則
為原點(diǎn),建立如圖所示的空間直角坐標(biāo)系.則![]() ,
,![]() ,
, ,
,![]() ,
,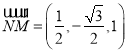 ,
,![]() ,
,![]() .
.
設(shè)平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() .
.
由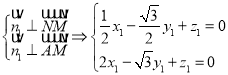 ,可取
,可取![]() ;
;
由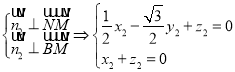 ,可取
,可取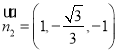 .
.
于是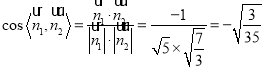 ,
,
所以二面角![]() 的正弦值是
的正弦值是![]() .
.


 通城學(xué)典默寫(xiě)能手系列答案
通城學(xué)典默寫(xiě)能手系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】[選修4—4:坐標(biāo)系與參數(shù)方程]
以平面直角坐標(biāo)系的原點(diǎn)為極點(diǎn),x軸的正半軸為極軸,建立極坐標(biāo)系,兩種坐標(biāo)系中取相同的長(zhǎng)度單位.已知直線(xiàn)l的參數(shù)方程是![]() (t為參數(shù)),圓C的極坐標(biāo)方程是ρ=4cos θ,求直線(xiàn)l被圓C截得的弦長(zhǎng).
(t為參數(shù)),圓C的極坐標(biāo)方程是ρ=4cos θ,求直線(xiàn)l被圓C截得的弦長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() 的最小值為
的最小值為![]() ,且對(duì)任意的
,且對(duì)任意的![]() ,不等式
,不等式![]() 恒成立,則實(shí)數(shù)m的最大值是________.
恒成立,則實(shí)數(shù)m的最大值是________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在直三棱柱ABC—A1B1C1中,ACBC,D,E分別是A1B1,BC的中點(diǎn).求證:

(1)平面ACD⊥平面BCC1B1;
(2)B1E∥平面ACD.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】明代商人程大位在公元1592年編撰完成《算法統(tǒng)宗》一書(shū).書(shū)中有如下問(wèn)題:“今有女子善織,初日遲,次日加倍,第三日轉(zhuǎn)速倍增,第四日又倍增,織成絹六丈七尺五寸.問(wèn)各日織若干?”意思是:“有一位女子善于織布,第一天由于不熟悉有點(diǎn)慢,第二天起每天織的布都是前一天的2倍,已知她前四天共織布6丈7尺5寸,問(wèn)這位女子每天織布多少?”根據(jù)文中的已知條件,可求得該女了第一天織布________尺,若織布一周(7天),共織________尺.(其中1丈為10尺,1尺為10寸)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】數(shù)據(jù)的收集和整理在當(dāng)今社會(huì)起到了舉足輕重的作用,它用統(tǒng)計(jì)的方法來(lái)幫助人們分析以往的行為習(xí)慣,進(jìn)而指導(dǎo)人們接下來(lái)的行動(dòng).
某支足球隊(duì)的主教練打算從預(yù)備球員甲、乙兩人中選一人為正式球員,他收集到了甲、乙兩名球員近期5場(chǎng)比賽的傳球成功次數(shù),如下表:
場(chǎng)次 | 第一場(chǎng) | 第二場(chǎng) | 第三場(chǎng) | 第四場(chǎng) | 第五場(chǎng) |
甲 | 28 | 33 | 36 | 38 | 45 |
乙 | 39 | 31 | 43 | 39 | 33 |
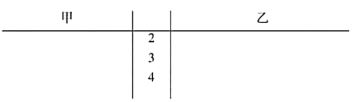
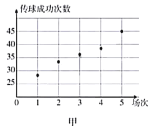
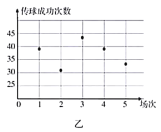
(1)根據(jù)這兩名球員近期5場(chǎng)比賽的傳球成功次數(shù),完成莖葉圖(莖表示十位,葉表示個(gè)位);分別在平面直角坐標(biāo)系中畫(huà)出兩名球員的傳球成功次數(shù)的散點(diǎn)圖;
(2)求出甲、乙兩名球員近期5場(chǎng)比賽的傳球成功次數(shù)的平均值和方差;
(3)主教練根據(jù)球員每場(chǎng)比賽的傳球成功次數(shù)分析出球員在場(chǎng)上的積極程度和技術(shù)水平,同時(shí)根據(jù)多場(chǎng)比賽的數(shù)據(jù)也可以分析出球員的狀態(tài)和潛力.你認(rèn)為主教練應(yīng)選哪位球員?并說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系xOy中曲線(xiàn)C的參數(shù)方程為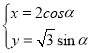 (
(![]() 為參數(shù)).以坐標(biāo)原點(diǎn)為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系,已知直線(xiàn)l過(guò)A,B兩點(diǎn),且這兩點(diǎn)的極坐標(biāo)分別為
為參數(shù)).以坐標(biāo)原點(diǎn)為極點(diǎn),x軸正半軸為極軸建立極坐標(biāo)系,已知直線(xiàn)l過(guò)A,B兩點(diǎn),且這兩點(diǎn)的極坐標(biāo)分別為![]() .
.
(I)求C的普通方程和![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(II)若M為曲線(xiàn)C上一動(dòng)點(diǎn),求點(diǎn)M到直線(xiàn)l的最小距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,直線(xiàn)C1的參數(shù)方程為![]() (t為參數(shù),0<α<π),曲線(xiàn)C2的參數(shù)方程為
(t為參數(shù),0<α<π),曲線(xiàn)C2的參數(shù)方程為 (φ為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系.
(φ為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系.
(1)求曲線(xiàn)C2的極坐標(biāo)方程;
(2)設(shè)曲線(xiàn)C1與曲線(xiàn)C2的交點(diǎn)分別為A,B,M(﹣2,0),求|MA|2+|MB|2的最大值及此時(shí)直線(xiàn)C1的傾斜角.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在如圖所示的多面體中,![]() 平面
平面![]() ,四邊形
,四邊形![]() 為平行四邊形,點(diǎn)
為平行四邊形,點(diǎn)![]() 分別為
分別為![]() 的中點(diǎn),且
的中點(diǎn),且![]() ,
,![]() ,
,![]() .
.
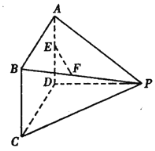
(1)求證:![]() 平面
平面![]() ;
;
(2)若![]() ,求該多面體的體積.
,求該多面體的體積.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com