
【題目】在極坐標系中,圓![]() 的極坐標方程為
的極坐標方程為![]() ,若以極點
,若以極點![]() 為原點,極軸所在的直線為
為原點,極軸所在的直線為![]() 軸建立平面直角坐標系
軸建立平面直角坐標系
(1)求圓![]() 的參數方程;
的參數方程;
(2)在直角坐標系中,點![]() 是圓
是圓![]() 上的動點,試求
上的動點,試求![]() 的最大值,并求出此時點
的最大值,并求出此時點![]() 的直角坐標;
的直角坐標;
(3)已知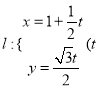 為參數),曲線
為參數),曲線![]() 為參數),若版曲線
為參數),若版曲線![]() 上各點恒坐標壓縮為原來的
上各點恒坐標壓縮為原來的![]() 倍,縱坐標壓縮為原來的
倍,縱坐標壓縮為原來的![]() 倍,得到曲線
倍,得到曲線![]() ,設點
,設點![]() 是曲線
是曲線![]() 上的一個動點,求它到直線
上的一個動點,求它到直線![]() 距離的最小值.
距離的最小值.
【答案】(1)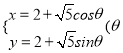 為參數);(2)最大值為
為參數);(2)最大值為![]() 時,點
時,點![]() 的直角坐標為
的直角坐標為![]() ;(3)
;(3)![]() .
.
【解析】試題分析:
(1)圓的普通方程為![]() ,所以所求圓
,所以所求圓![]() 的參數方程為
的參數方程為 為參數).
為參數).
(2) 設![]() ,代入
,代入![]()
整理可知則關于![]() 的方程必有實數根,
的方程必有實數根,
所以![]() ,解得
,解得![]() ,即
,即![]() 的最大值為11,
的最大值為11,
故![]() 的最大值為
的最大值為![]() 時,點
時,點![]() 的直角坐標為
的直角坐標為![]() .
.
(3)點![]() 的坐標是
的坐標是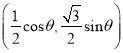 ,
, ![]() ,
,
當![]() 時,
時, ![]() 取得最小值,
取得最小值, ![]() .
.
試題解析:(1)因為![]() ,所以
,所以![]() ,
,
即![]() 為圓
為圓![]() 的普通方程,
的普通方程,
所以所求圓![]() 的參數方程為
的參數方程為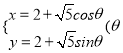 為參數).
為參數).
(2)設![]() ,得
,得![]() 代入
代入![]()
整理得![]() ,則關于
,則關于![]() 的方程必有實數根,
的方程必有實數根,
所以![]() ,化簡得
,化簡得![]() ,
,
解得![]() ,即
,即![]() 的最大值為11,
的最大值為11,
將![]() 代入方程,得
代入方程,得![]() ,解得
,解得![]() ,代入
,代入![]() 得
得![]() ,
,
故![]() 的最大值為
的最大值為![]() 時,點
時,點![]() 的直角坐標為
的直角坐標為![]() .
.
(3)![]() 的參數方程為
的參數方程為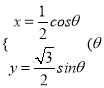 為參數),故點
為參數),故點![]() 的坐標是
的坐標是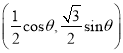 ,
,
從而點![]() 到直線
到直線![]() 的距離是
的距離是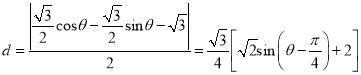 ,
,
由此當![]() 時,
時, ![]() 取得最小值,且最小值為
取得最小值,且最小值為![]() .
.


科目:高中數學 來源: 題型:
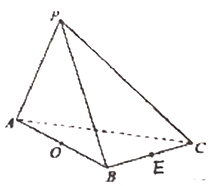
【題目】在三棱錐![]() 中,
中, ![]() 和
和![]() 是邊長為
是邊長為![]() 的等邊三角形,
的等邊三角形, ![]() ,
, ![]() 是
是![]() 中點,
中點, ![]() 是
是![]() 中點.
中點.
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(Ⅲ)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 的余弦值為
的余弦值為![]() ?若存在,指出點
?若存在,指出點![]() 在
在![]() 上的位置;若不存在,說明理由.
上的位置;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位從一所學校招收某類特殊人才,對20位已經選拔入圍的學生進行運動協調能力和邏輯思維能力的測試,其測試結果如下表:
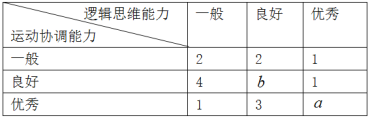
例如表中運動協調能力良好且邏輯思維能力一般的學生是4人,由于部分數據丟失,只知道從這20位參加測試的學生中隨機抽取一位,抽到邏輯思維能力優秀的學生的概率為![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
(2)從運動協調能力為優秀的學生中任意抽取2位,求其中至少有一位邏輯思維能力優秀的學生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交強險是車主必須為機動車購買的險種,若普通![]() 座以下私家車投保交強險第一年的費用(基準保費)統一為
座以下私家車投保交強險第一年的費用(基準保費)統一為![]() 元,在下一年續保時,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系,發生交通事故的次數越多,費率也就越高,具體浮動情況如下表:
元,在下一年續保時,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系,發生交通事故的次數越多,費率也就越高,具體浮動情況如下表:

某機構為了研究某一品牌普通![]() 座以下私家車的投保情況,隨機抽取了
座以下私家車的投保情況,隨機抽取了![]() 輛車齡已滿三年的該品牌同型號私家車的下一年續保時的情況,統計得到了下面的表格:
輛車齡已滿三年的該品牌同型號私家車的下一年續保時的情況,統計得到了下面的表格:
類型 |
|
|
|
|
|
|
數量 | 10 | 5 | 5 | 20 | 15 | 5 |
以這![]() 輛該品牌車的投保類型的頻率代替一輛車投保類型的概率,完成下列問題:
輛該品牌車的投保類型的頻率代替一輛車投保類型的概率,完成下列問題:
(Ⅰ)按照我國《機動車交通事故責任強制保險條例》汽車交強險價格的規定, ![]() ,記
,記![]() 為某同學家里的一輛該品牌車在第四年續保時的費用,求
為某同學家里的一輛該品牌車在第四年續保時的費用,求![]() 的分布列與數學期望;(數學期望值保留到個位數字)
的分布列與數學期望;(數學期望值保留到個位數字)
(Ⅱ)某二手車銷售商專門銷售這一品牌的二手車,且將下一年的交強險保費高于基本保費的車輛記為事故車,假設購進一輛事故車虧損![]() 元,一輛非事故車盈利
元,一輛非事故車盈利![]() 元:
元:
①若該銷售商購進三輛(車齡已滿三年)該品牌二手車,求這三輛車中至少有一輛事故車的概率;
②若該銷售商一次購進![]() 輛(車齡已滿三年)該品牌二手車,求他獲得利潤的期望值.
輛(車齡已滿三年)該品牌二手車,求他獲得利潤的期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
(Ⅰ)討論函數![]() 的單調區間與極值;
的單調區間與極值;
(Ⅱ)若![]() 且
且![]() 恒成立,求
恒成立,求![]() 的最大值;
的最大值;
(Ⅲ)在(Ⅱ)的條件下,且![]() 取得最大值時,設
取得最大值時,設![]() ,且函數
,且函數![]() 有兩個零點
有兩個零點![]() ,求實數
,求實數![]() 的取值范圍,并證明:
的取值范圍,并證明: ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com