
【題目】某同學(xué)用“五點(diǎn)法”畫函數(shù)![]() 在某一周期內(nèi)的圖像時(shí),列表并填入的部分?jǐn)?shù)據(jù)如下表:
在某一周期內(nèi)的圖像時(shí),列表并填入的部分?jǐn)?shù)據(jù)如下表:
|
|
|
|
|
|
| 0 |
|
|
|
|
| 0 | 1 | 0 |
| 0 |
| 0 |
| 0 |
| 0 |
(1)請(qǐng)寫出上表的![]() 及函數(shù)
及函數(shù)![]() 的解析式;
的解析式;
(2)將函數(shù)![]() 的圖像向右平移
的圖像向右平移![]() 個(gè)單位,再將所得圖像上各點(diǎn)的橫坐標(biāo)縮小為原來(lái)的
個(gè)單位,再將所得圖像上各點(diǎn)的橫坐標(biāo)縮小為原來(lái)的![]() ,縱坐標(biāo)不變,得到函數(shù)
,縱坐標(biāo)不變,得到函數(shù)![]() 的圖像,求
的圖像,求![]() 的解析式及
的解析式及 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(3)在(2)的條件下,若![]() 在
在![]() 上恰有奇數(shù)個(gè)零點(diǎn),求實(shí)數(shù)
上恰有奇數(shù)個(gè)零點(diǎn),求實(shí)數(shù)![]() 與零點(diǎn)個(gè)數(shù)
與零點(diǎn)個(gè)數(shù)![]() 的值.
的值.
【答案】(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
【解析】
(1)根據(jù)表中數(shù)據(jù)可得關(guān)于![]() 的方程組,解出
的方程組,解出![]() 的值后可得
的值后可得![]() 的值,再由表中數(shù)據(jù)可得
的值,再由表中數(shù)據(jù)可得![]() ,從而可得函數(shù)的解析式.
,從而可得函數(shù)的解析式.
(2)先求出![]() 的解析式,再求出
的解析式,再求出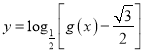 的定義域,結(jié)合三角函數(shù)的單調(diào)性可得復(fù)合函數(shù)的單調(diào)增區(qū)間.
的定義域,結(jié)合三角函數(shù)的單調(diào)性可得復(fù)合函數(shù)的單調(diào)增區(qū)間.
(3)令![]() ,設(shè)方程
,設(shè)方程![]() 的根為
的根為![]() ,分①
,分①![]() ;②
;②![]() ;③
;③![]() 三種情況討論
三種情況討論![]() 在
在![]() 及
及![]() 上零點(diǎn)個(gè)數(shù),再根據(jù)周期性得到
上零點(diǎn)個(gè)數(shù),再根據(jù)周期性得到![]() 的零點(diǎn)個(gè)數(shù),結(jié)合題設(shè)條件可得
的零點(diǎn)個(gè)數(shù),結(jié)合題設(shè)條件可得![]() 的值及相應(yīng)的零點(diǎn)個(gè)數(shù).
的值及相應(yīng)的零點(diǎn)個(gè)數(shù).
(1)根據(jù)表中的數(shù)據(jù)可得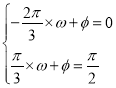 ,解得
,解得 ,
,
故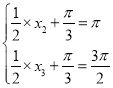 ,所以
,所以 ,又
,又![]() ,故
,故![]() .
.
所以![]() .
.
(2)將函數(shù)![]() 的圖像向右平移
的圖像向右平移![]() 個(gè)單位,所得圖像的解析式為:
個(gè)單位,所得圖像的解析式為:
![]() ,
,
再將所得圖像上各點(diǎn)的橫坐標(biāo)縮小為原來(lái)的![]() ,縱坐標(biāo)不變,得到函數(shù)
,縱坐標(biāo)不變,得到函數(shù)![]() 的圖像,
的圖像,
故![]() .
.
此時(shí)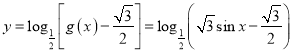 ,
,
令![]() ,則
,則![]() ,故
,故![]() .
.
當(dāng)![]() 時(shí),
時(shí),![]() 為增函數(shù),
為增函數(shù),
故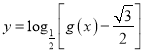 為減函數(shù);
為減函數(shù);
當(dāng)![]() 時(shí),
時(shí),![]() 為減函數(shù);
為減函數(shù);
故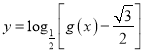 為增函數(shù).
為增函數(shù).
所以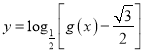 的增區(qū)間為
的增區(qū)間為![]() .
.
(3)![]() ,
,![]() 的周期為
的周期為![]() ,
,
當(dāng)![]() 時(shí),令
時(shí),令![]() ,考慮方程
,考慮方程![]() 的根情況,
的根情況,
因![]() ,故
,故![]() 在
在![]() 必有兩個(gè)不同的實(shí)數(shù)根
必有兩個(gè)不同的實(shí)數(shù)根![]() ,
,
因?yàn)?/span>![]() 在
在![]() 有奇數(shù)個(gè)零點(diǎn),故
有奇數(shù)個(gè)零點(diǎn),故![]() 或
或![]() .
.
若![]() ,則方程
,則方程![]() 、
、![]() 在
在![]() 共有4個(gè)不同的實(shí)數(shù)根,
共有4個(gè)不同的實(shí)數(shù)根,
在![]() 有0個(gè)實(shí)數(shù)根或2個(gè)實(shí)數(shù)根,
有0個(gè)實(shí)數(shù)根或2個(gè)實(shí)數(shù)根,
故![]() 在
在![]() 有
有![]() 個(gè)根或
個(gè)根或![]() 個(gè)根,
個(gè)根,
與![]() 有奇數(shù)個(gè)零點(diǎn)矛盾,舍去.
有奇數(shù)個(gè)零點(diǎn)矛盾,舍去.
若![]() ,則
,則![]() 在
在![]() 共有2個(gè)不同的實(shí)數(shù)根,在
共有2個(gè)不同的實(shí)數(shù)根,在![]() 有0個(gè)實(shí)數(shù)根或2個(gè)實(shí)數(shù)根,
有0個(gè)實(shí)數(shù)根或2個(gè)實(shí)數(shù)根,
故![]() 在
在![]() 有
有
![]() 個(gè)根或
個(gè)根或![]() ,
,
與![]() 有奇數(shù)個(gè)零點(diǎn)矛盾,舍去.
有奇數(shù)個(gè)零點(diǎn)矛盾,舍去.
同理![]() 也不成立,所以
也不成立,所以![]() 或
或![]() ,
,
若![]() ,則
,則![]() ,
,![]() ,
,
方程![]() 、
、![]() 在
在![]() 共有3個(gè)不同的實(shí)數(shù)根,而在
共有3個(gè)不同的實(shí)數(shù)根,而在![]() 上,
上,![]() 有兩個(gè)不同的根,
有兩個(gè)不同的根,![]() 無(wú)解,
無(wú)解,
所以![]() 在
在![]() 有
有![]() 個(gè)根,符合要求;
個(gè)根,符合要求;
若![]() ,則
,則![]() ,
,![]() ,
,
方程![]() 、
、![]() 在
在![]() 共有3個(gè)不同的實(shí)數(shù)根,而在
共有3個(gè)不同的實(shí)數(shù)根,而在![]() 上,
上,![]() 無(wú)解,
無(wú)解,![]() 有一個(gè)根,
有一個(gè)根,
所以故![]() 在
在![]() 有
有![]() 個(gè)根,與題設(shè)矛盾,舍去.
個(gè)根,與題設(shè)矛盾,舍去.
綜上,![]() ,
,![]() 在
在![]() 共有
共有![]() 個(gè)不同的零點(diǎn).
個(gè)不同的零點(diǎn).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)ω>0,函數(shù)y=2cos(ωx+ ![]() )﹣1的圖象向右平移
)﹣1的圖象向右平移 ![]() 個(gè)單位后與原圖象重合,則ω的最小值是( )
個(gè)單位后與原圖象重合,則ω的最小值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某知名品牌汽車深受消費(fèi)者喜愛(ài),但價(jià)格昂貴.某汽車經(jīng)銷商推出A、B、C三種分期付款方式銷售該品牌汽車,并對(duì)近期100位采用上述分期付款的客戶進(jìn)行統(tǒng)計(jì)分析,得到如下的柱狀圖.已知從A、B、C三種分期付款銷售中,該經(jīng)銷商每銷售此品牌汽車1倆所獲得的利潤(rùn)分別是1萬(wàn)元,2萬(wàn)元,3萬(wàn)元.現(xiàn)甲乙兩人從該汽車經(jīng)銷商處,采用上述分期付款方式各購(gòu)買此品牌汽車一輛.以這100位客戶所采用的分期付款方式的頻率代替1位客戶采用相應(yīng)分期付款方式的概率.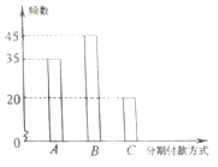
(1)求甲乙兩人采用不同分期付款方式的概率;
(2)記X(單位:萬(wàn)元)為該汽車經(jīng)銷商從甲乙兩人購(gòu)車中所獲得的利潤(rùn),求X的分布列與期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2015![]() 全國(guó)統(tǒng)考II)設(shè)函數(shù)f(x)=ln(1+|x|)-
全國(guó)統(tǒng)考II)設(shè)函數(shù)f(x)=ln(1+|x|)-![]() ,則使得f(x)
,則使得f(x)![]() f(2x-1)成立的x的取值范圍是()
f(2x-1)成立的x的取值范圍是()
A.(![]() ,1)
,1)
B.(-![]() ,
,![]() )
)![]() (1,+
(1,+![]() )
)
C.(-![]() ,
,![]() )
)
D.(-![]() ,-
,-![]() )
)![]() (
(![]() ,+
,+![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】![]() 在直角坐標(biāo)系xOy中,曲線C1:
在直角坐標(biāo)系xOy中,曲線C1:![]() (t為參數(shù),且t≠0),其中0
(t為參數(shù),且t≠0),其中0![]()
![]()
![]() , 在以O(shè)為極點(diǎn)x軸正半軸為極軸的極坐標(biāo)系中,曲線C2::
, 在以O(shè)為極點(diǎn)x軸正半軸為極軸的極坐標(biāo)系中,曲線C2::![]() =2sin
=2sin![]() , C3:
, C3:![]() =2
=2![]() cos
cos![]()
(1)求C2與C3交點(diǎn)的直角坐標(biāo)
(2)若C1與C2相交于點(diǎn)A,C1與C3相交于點(diǎn)B,求|AB|最大值
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某旅行社組織一批游客外出旅游,原計(jì)劃租用45座客車若干輛,但有15人沒(méi)有座位;若租用同樣數(shù)量的60座客車,則多出一輛車,且其余客車恰好坐滿,已知45座客車租金為每輛220元,60座客車租金為每輛300元,問(wèn):
(1)這批游客的人數(shù)是多少?原計(jì)劃租用多少輛45座客車?
(2)若租用同一種車,要使每位游客都有座位,應(yīng)該怎樣租用才合算?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2015·新課標(biāo)I卷)如圖,四邊形ABCD為菱形,∠ABC=120°,E , F是平面ABCD同一側(cè)的兩點(diǎn),BE⊥平面ABCD , DF⊥平面ABCD , BE=2DF , AE⊥EC.
(1)證明:平面AEC⊥平面AFC
(2)求直線AE與直線CF所成角的余弦值
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2015·四川)已知函數(shù)f(x)=2x , g(x)=x2+ax(其中a![]() R).對(duì)于不相等的實(shí)數(shù)x1, x2 , 設(shè)m=
R).對(duì)于不相等的實(shí)數(shù)x1, x2 , 設(shè)m=![]() ,n=
,n=![]() .
.
現(xiàn)有如下命題:
(1)對(duì)于任意不相等的實(shí)數(shù)x1, x2 , 都有m>0;
(2)對(duì)于任意的a及任意不相等的實(shí)數(shù)x1, x2 , ,都有n>0;
(3)對(duì)于任意的a , 存在不相等的實(shí)數(shù)x1, x2 , 使得m=n;
(4)對(duì)于任意的a , 存在不相等的實(shí)數(shù)x1, x2 , 使得m=-n.
其中的真命題有 (寫出所有真命題的序號(hào)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2015·湖南)某商場(chǎng)舉行有獎(jiǎng)促銷活動(dòng),顧客購(gòu)買一定金額的商品后即可抽獎(jiǎng),抽獎(jiǎng)方法是:從裝有2個(gè)紅球A1, A2和1個(gè)白球B的甲箱與裝有2個(gè)紅球a1,a2和2個(gè)白球b1,b2的乙箱中,各隨機(jī)摸出1個(gè)球,若摸出的2個(gè)球都是紅球則中獎(jiǎng),否則不中獎(jiǎng)。
(1)用球的標(biāo)號(hào)列出所有可能的摸出結(jié)果;
(2)有人認(rèn)為:兩個(gè)箱子中的紅球比白球多,所以中獎(jiǎng)的概率大于不中獎(jiǎng)的概率,你認(rèn)為正確嗎?請(qǐng)說(shuō)明理由。
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com