
【題目】如圖,在△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC內(nèi)的一點(diǎn).
,AC=3, BC=2,P是△ABC內(nèi)的一點(diǎn).

(1)若△BPC是以BC為斜邊的等腰直角三角形,求PA長;
(2)若∠BPC=![]() ,求△PBC面積的最大值.
,求△PBC面積的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由三角形![]() 為等腰直角三角形,利用勾股定理求出
為等腰直角三角形,利用勾股定理求出![]() 的長,在三角形
的長,在三角形![]() 中,利用余弦定理求出的
中,利用余弦定理求出的![]() 長即可;(2)在三角形
長即可;(2)在三角形![]() 中,由
中,由![]() 的度數(shù)表示出
的度數(shù)表示出![]() 的度數(shù),利用正弦定理表示出
的度數(shù),利用正弦定理表示出![]() 與
與![]() ,進(jìn)而表示出三角形
,進(jìn)而表示出三角形![]() 面積,利用正弦函數(shù)的值域確定出面積的最大值即可.
面積,利用正弦函數(shù)的值域確定出面積的最大值即可.
(1)由題設(shè),∠PCA=![]() ,PC=
,PC=![]() ,在△PAC中,由余弦定理得
,在△PAC中,由余弦定理得
PA2=AC2+PC2-2AC·PCcos![]() =5,于是PA=
=5,于是PA=![]() .
.
(2)∠BPC=![]() ,設(shè)∠PCB=θ,則θ∈(0,
,設(shè)∠PCB=θ,則θ∈(0,![]() ).
).
在△PBC中,∠PBC=![]() -θ.由正弦定理得
-θ.由正弦定理得![]() =
=![]() =
=![]() ,
,
得PB=![]() sinθ,PC=
sinθ,PC=![]() sin(
sin(![]() -θ).
-θ).
所以△PBC面積S=![]() PB·PCsin
PB·PCsin![]() =
=![]() sin (
sin (![]() -θ)sinθ=
-θ)sinθ=![]() sin(2θ+
sin(2θ+![]() )-
)-![]() .
.
當(dāng)θ=![]() ∈(0,
∈(0,![]() )時,△PBC面積的最大值為
)時,△PBC面積的最大值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】數(shù)列{an}中,a1=8,a4=2,且滿足an+2-2an+1+an=0.
(1)求數(shù)列的通項公式;
(2)設(shè)Sn=|a1|+|a2|+…+|an|,求Sn.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在等腰直角![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在線段
在線段![]() 上.
上.

(Ⅰ) 若![]() ,求
,求![]() 的長;
的長;
(Ⅱ)若點(diǎn)![]() 在線段
在線段![]() 上,且
上,且![]() ,問:當(dāng)
,問:當(dāng)![]() 取何值時,
取何值時,![]() 的面積最小?并求出面積的最小值.
的面積最小?并求出面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了更好地規(guī)劃進(jìn)貨的數(shù)量,保證蔬菜的新鮮程度,某蔬菜商店從某一年的銷售數(shù)據(jù)中,隨機(jī)抽取了8組數(shù)據(jù)作為研究對象,如右下表所示(![]() (噸)為買進(jìn)蔬菜的質(zhì)量,
(噸)為買進(jìn)蔬菜的質(zhì)量,![]() (天)為銷售天數(shù)):
(天)為銷售天數(shù)):
(Ⅰ) 根據(jù)右表提供的數(shù)據(jù)在網(wǎng)格中繪制散點(diǎn)圖,并判斷![]() 與
與![]() 是否線性相關(guān),若線性相關(guān),用最小二乘法求出
是否線性相關(guān),若線性相關(guān),用最小二乘法求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]()

| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅱ)根據(jù)(Ⅰ)中的計算結(jié)果,若該蔬菜商店準(zhǔn)備一次性買進(jìn)蔬菜25噸,則預(yù)計需要銷售多少天.
參考公式: ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,直線l的參數(shù)方程為 (其中t為參數(shù)).現(xiàn)以坐標(biāo)原點(diǎn)為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為ρ=6cosθ.
(其中t為參數(shù)).現(xiàn)以坐標(biāo)原點(diǎn)為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為ρ=6cosθ.
(Ⅰ)寫出直線l普通方程和曲線C的直角坐標(biāo)方程;
(Ⅱ)過點(diǎn)M(-1,0)且與直線l平行的直線l1交C于A,B兩點(diǎn),求|AB|.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】關(guān)于函數(shù)![]() 有下述四個結(jié)論:①若
有下述四個結(jié)論:①若![]() ,則
,則![]() ;②
;②![]() 的圖象關(guān)于點(diǎn)
的圖象關(guān)于點(diǎn)![]() 對稱;③函數(shù)
對稱;③函數(shù)![]() 在
在![]() 上單調(diào)遞增;④
上單調(diào)遞增;④![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后所得圖象關(guān)于
個單位長度后所得圖象關(guān)于![]() 軸對稱.其中所有正確結(jié)論的編號是( )
軸對稱.其中所有正確結(jié)論的編號是( )
A.①②④B.①②C.③④D.②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在極坐標(biāo)系中,已知曲線![]() ,將曲線
,將曲線![]() 上的點(diǎn)向左平移一個單位,然后縱坐標(biāo)不變,橫坐標(biāo)軸伸長到原來的2倍,得到曲線
上的點(diǎn)向左平移一個單位,然后縱坐標(biāo)不變,橫坐標(biāo)軸伸長到原來的2倍,得到曲線![]() ,又已知直線
,又已知直線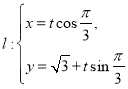 (
(![]() 是參數(shù)),且直線
是參數(shù)),且直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點(diǎn).
兩點(diǎn).
(I)求曲線![]() 的直角坐標(biāo)方程,并說明它是什么曲線;
的直角坐標(biāo)方程,并說明它是什么曲線;
(II)設(shè)定點(diǎn)![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中, ![]() ,
, ![]() 平面
平面![]() ,側(cè)面
,側(cè)面![]() 是正方形,點(diǎn)
是正方形,點(diǎn)![]() 為棱
為棱![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 、
、![]() 分別在棱
分別在棱![]() 、
、![]() 上,且
上,且![]() ,
, ![]() .
.
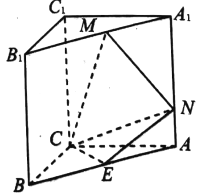
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com