【題目】在△ABC中，角A、B、C對應的邊分別為a、b、c，已知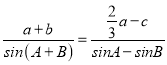
．
（1）求cosB的值；
（2）若b＝8，cos2A﹣3cos（B+C）＝1，求△ABC的面積．
【答案】（1）
（2）6
8
【解析】
（1）利用正弦定理及誘導公式整理已知可得：
，結合余弦定理得解。
（2）化簡，cos2A﹣3cos（B+C）＝1可得：2cos2A+3cosA﹣2＝0，即可求得cosA
，sinA
，利用兩角和的正弦公式可得： 
，再利用正弦定理列方程求得a＝3
，再利用三角形面積公式計算得解。
解：（1）由
得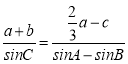
，
由正弦定理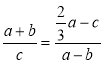得：
，變形得，所以cosB
．
（2）由cos2A﹣3cos（B+C）＝1得2cos2A+3cosA﹣2＝0，解得cosA，∴A
，
∴sinA，又sinB
，
∴sinC＝sin（A+B）＝sinAcosB+cosAsinB
，
由正弦定理得
，得a＝3，
所以三角形ABC的面積為
absinC
8
6
8
．
能考試期末沖刺卷系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
+ 
=1（a＞b＞0）的左、右焦點分別為F1、F2 ， 橢圓C過點P（1， 
），直線PF1交y軸于Q，且 
=2 
，O為坐標原點．
（1）求橢圓C的方程；
（2）設M是橢圓C的上頂點，過點M分別作直線MA，MB交橢圓C于A，B兩點，設這兩條直線的斜率分別為k1 ， k2 ， 且k1+k2=2，證明：直線AB過定點．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】知雙曲線 
﹣ 
=1（a＞0，b＞0），A1、A2是實軸頂點，F是右焦點，B（0，b）是虛軸端點，若在線段BF上（不含端點）存在不同的兩點Pi=（1，2），使得△PiA1A2（i=1，2）構成以A1A2為斜邊的直角三角形，則雙曲線離心率e的取值范圍是（ ）
A.（ 
， 
）
B.（ ， 
）
C.（1， ）
D.（ ，+∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列判斷錯誤的是
A. 若隨機變量
服從正態分布
,則
；
B. 若
組數據
的散點都在
上，則相關系數
；
C. 若隨機變量服從二項分布： 
, 則
；
D. 
是
的充分不必要條件；
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示的幾何體ABCDE中，DA⊥平面EAB，CB∥DA，EA=DA=AB=2CB，EA⊥ AB，M是EC上的點（不與端點重合），F為DA上的點，N為BE的中點．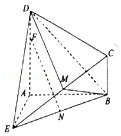
（Ⅰ）若M是EC的中點，AF=3FD，求證：FN∥平面MBD；
（Ⅱ）若平面MBD與平面ABD所成角（銳角）的余弦值為 
，試確定點M在EC上的位置．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
的前
項和為
，滿足
，
．數列
滿足
，，且
．
（1）求數列和的通項公式；
（2）若
，數列
的前項和為
，對任意的，都有
，求實數
的取值范圍；
（3）是否存在正整數
，，使
，
，
（
）成等差數列，若存在，求出所有滿足條件的，，若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
，
，若
對任意
成立，則下列命題中正確的命題個數是（ ）
（1）
（2）
（3）
不具有奇偶性
（4）的單調增區間是
（5）可能存在經過點
的直線與函數的圖象不相交
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
