考點:三角函數中的恒等變換應用
專題:三角函數的圖像與性質
分析:(1)函數f(x)可化簡為f(x)=2sin(2x-
),從而可求最小正周期及在區間[0,
]上的最大值和最小值;
(2)先求出sin(2x
0-),cos(2x
0-)的值,從而cos2x
0=cos[(2x
0-)+
]=-
.
解答:
解:(1)由f(x)=2cosx(
sinx-cosx)+1(x∈R)得
f(x)=
(2sinxcosx)-(2cos
2x-1)=
sin2x-cos2x=2sin(2x-
)
所以函數f(x)的最小正周期為π
因為f(x)=2sin(2x-
)在區間[0,
]上是增函數,在區間[
,
]上為減函數,
又f(0)=-1,f(
)=2,f(
)=
,
所以函數f(x)在區間[0,
]上的最大值為2,最小值為-1.
(Ⅱ)解:由(1)可知f(x
0)=2sin(2x
0-)
又因為f(x
0)=
,所以sin(2x
0-)=
由x
0∈[
,
],得2x
0-∈[
,π]
從而cos(2x
0-)=-
=-
所以cos2x
0=cos[(2x
0-)+
]=cos(2x
0-)cos
-sin(2x
0-)sin
=-
點評:本題主要考察了三角函數中的恒等變換應用,三角函數的圖象與性質,屬于基礎題.



 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案 一課一練一本通系列答案
一課一練一本通系列答案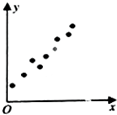 已知變量x與y呈相關關系,且由觀測數據得到的樣本數據散點圖如圖所示,則由該觀測數據算得的回歸方程可能是( )
已知變量x與y呈相關關系,且由觀測數據得到的樣本數據散點圖如圖所示,則由該觀測數據算得的回歸方程可能是( )