
【題目】設橢圓中心在坐標原點,![]() 是它的兩個頂點,直線
是它的兩個頂點,直線![]() 與AB相交于點D,與橢圓相交于E、F兩點.
與AB相交于點D,與橢圓相交于E、F兩點.
(Ⅰ)若![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求四邊形![]() 面積的最大值.
面積的最大值.
【答案】(Ⅰ)解:依題設得橢圓的方程為![]() ,
,
直線![]() 的方程分別為
的方程分別為![]() ,
,![]() .············ 2分
.············ 2分
如圖,設![]() ,其中
,其中![]() ,
,

且![]() 滿足方程
滿足方程![]() ,故
,故![]() .①
.①
由![]() 知
知![]() ,得
,得![]() ;
;
由![]() 在
在![]() 上知
上知![]() ,得
,得![]() .所以
.所以![]() ,
,
化簡得![]() ,解得
,解得![]() 或
或![]() .················ 6分
.················ 6分
(Ⅱ)根據(jù)點到直線的距離公式和①式知,點![]() 到
到![]() 的距離分別為
的距離分別為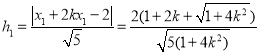 ,
,
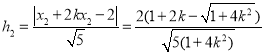 .9分
.9分
又![]() ,所以四邊形
,所以四邊形![]() 的面積為
的面積為
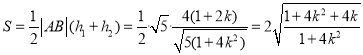
![]() ,
,
當![]() ,即當
,即當![]() 時,上式取等號.所以
時,上式取等號.所以![]() 的最大值為
的最大值為![]() .
.
【解析】
試題(Ⅰ)由題意易得橢圓方程,直線![]() 的方程,再設
的方程,再設![]() ,
,![]() 滿足方程
滿足方程![]() ,把
,把![]() 用坐標表示出來得
用坐標表示出來得![]() ,又點
,又點![]() 在直線
在直線![]() 上,則
上,則![]() ,根據(jù)以上關系式可解得
,根據(jù)以上關系式可解得![]() 的值;(Ⅱ)先求點E、F到AB的距離,再求
的值;(Ⅱ)先求點E、F到AB的距離,再求![]() ,則可得面積
,則可得面積![]() ,然后利用不等式求面積的最大值.
,然后利用不等式求面積的最大值.
試題解析:(I)依題意,得橢圓的方程為![]() , 1分
, 1分
直線![]() 的方程分別為
的方程分別為![]() , 2分
, 2分
如圖設![]() ,其中
,其中![]() ,
,
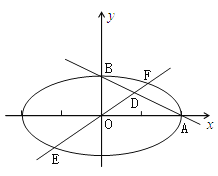
![]() 滿足方程
滿足方程![]() 且故
且故![]() ,
,
由![]() 知
知![]() ,得
,得![]() , 4分
, 4分
由點![]() 在直線
在直線![]() 上知,
上知,![]() 得
得![]() , 5分
, 5分
![]() ,化簡得
,化簡得![]() 解得
解得![]() 或
或![]() . 7分
. 7分
(II)根據(jù)點到直線的距離公式和①式知,點E、F到AB的距離分別為
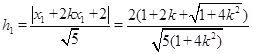 , 8分
, 8分
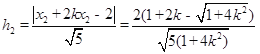 , 9分
, 9分
又![]() ,所以四邊形AEBF的面積為
,所以四邊形AEBF的面積為
![]()
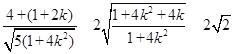 , 11分
, 11分
當![]() 即當
即當![]() 時,上式取等號,所以S的最大值為
時,上式取等號,所以S的最大值為![]() 13分
13分


科目:高中數(shù)學 來源: 題型:
【題目】對于任意的復數(shù)![]() ,定義運算
,定義運算![]() 為
為![]() .
.
(1)設集合![]() {
{![]() 均為整數(shù)},用列舉法寫出集合
均為整數(shù)},用列舉法寫出集合![]() ;
;
(2)若![]() ,
,![]() 為純虛數(shù),求
為純虛數(shù),求![]() 的最小值;
的最小值;
(3)問:直線![]() 上是否存在橫坐標、縱坐標都為整數(shù)的點,使該點
上是否存在橫坐標、縱坐標都為整數(shù)的點,使該點![]() 對應的復數(shù)
對應的復數(shù)![]() 經運算
經運算![]() 后,
后,![]() 對應的點也在直線
對應的點也在直線![]() 上?若存在,求出所有的點;若不存在,請說明理由.
上?若存在,求出所有的點;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】從1,3,5,7,9中任取3個數(shù)宇,與0,2,4組成沒有重復數(shù)字的六位數(shù),其中偶數(shù)共有( )
A.312個B.1560個C.2160個D.3120個
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某高中志愿者部有男志愿者6人,女志愿者4人,這些人要參加元旦聯(lián)歡會的服務工作. 從這些人中隨機抽取4人負責舞臺服務工作,另外6人負責會場服務工作.
(Ⅰ)設![]() 為事件:“負責會場服務工作的志愿者中包含女志愿者
為事件:“負責會場服務工作的志愿者中包含女志愿者![]() 但不包含男志愿者
但不包含男志愿者![]() ”,求事件
”,求事件![]() 發(fā)生的概率.
發(fā)生的概率.
(Ⅱ)設![]() 表示參加舞臺服務工作的女志愿者人數(shù),求隨機變量
表示參加舞臺服務工作的女志愿者人數(shù),求隨機變量![]() 的分布列與數(shù)學期望.
的分布列與數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】對于給定數(shù)列![]() ,如果存在實常數(shù)
,如果存在實常數(shù)![]() 使得
使得![]() 對于任意
對于任意![]() 都成立,我們稱數(shù)列
都成立,我們稱數(shù)列![]() 是“M類數(shù)列”.
是“M類數(shù)列”.
(1)若![]() ,數(shù)列
,數(shù)列![]() 是否為“M類數(shù)列”?若是,指出它對應的實常數(shù)
是否為“M類數(shù)列”?若是,指出它對應的實常數(shù)![]() ;若不是,請說明理由;
;若不是,請說明理由;
(2)證明:若數(shù)列![]() 是“M類數(shù)列”,則數(shù)列
是“M類數(shù)列”,則數(shù)列![]() 也是“M類數(shù)列”.
也是“M類數(shù)列”.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com