
【題目】如圖,已知城市![]() 周邊有兩個小鎮(zhèn)
周邊有兩個小鎮(zhèn)![]() 、
、![]() ,其中鄉(xiāng)鎮(zhèn)
,其中鄉(xiāng)鎮(zhèn)![]() 位于城市
位于城市![]() 的正東方
的正東方![]() 處,鄉(xiāng)鎮(zhèn)
處,鄉(xiāng)鎮(zhèn)![]() 與城市
與城市![]() 相距
相距![]() ,
,![]() 與
與![]() 夾角的正切值為2,為方便交通,現(xiàn)準(zhǔn)備建設(shè)一條經(jīng)過城市
夾角的正切值為2,為方便交通,現(xiàn)準(zhǔn)備建設(shè)一條經(jīng)過城市![]() 的公路
的公路![]() ,使鄉(xiāng)鎮(zhèn)
,使鄉(xiāng)鎮(zhèn)![]() 和
和![]() 分別位于
分別位于![]() 的兩側(cè),過
的兩側(cè),過![]() 和
和![]() 建設(shè)兩條垂直
建設(shè)兩條垂直![]() 的公路
的公路![]() 和
和![]() ,分別與公路
,分別與公路![]() 交匯于
交匯于![]() 、
、![]() 兩點,以
兩點,以![]() 為原點,
為原點,![]() 所在直線為
所在直線為![]() 軸,建立如圖所示的平面直角坐標(biāo)系
軸,建立如圖所示的平面直角坐標(biāo)系![]() .
.

(1)當(dāng)兩個交匯點![]() 、
、![]() 重合,試確定此時
重合,試確定此時![]() 路段長度;
路段長度;
(2)當(dāng)![]() ,計算此時兩個交匯點
,計算此時兩個交匯點![]() 、
、![]() 到城市
到城市![]() 的距離之比;
的距離之比;
(3)若要求兩個交匯點![]() 、
、![]() 的距離不超過
的距離不超過![]() ,求
,求![]() 正切值的取值范圍.
正切值的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)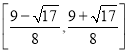 .
.
【解析】
(1)先求出直線![]() 的斜率為1,點B的坐標(biāo)為
的斜率為1,點B的坐標(biāo)為![]() ,再利用點到直線的距離為|BD|=
,再利用點到直線的距離為|BD|=![]() ;(2)設(shè)直線AB的斜率為
;(2)設(shè)直線AB的斜率為![]() ,先求出
,先求出![]() 再求出
再求出![]() ,即得
,即得![]() ;(3)先求出
;(3)先求出![]() ,再求出
,再求出![]() 解不等式即得解.
解不等式即得解.
(1)當(dāng)兩個交匯點![]() 、
、![]() 重合時,則AC,BD公路共線,
重合時,則AC,BD公路共線,
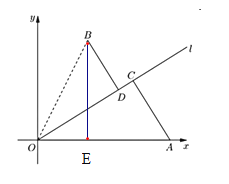
過點B作BE⊥AO,垂足為E, 則![]() ,
,
所以AE=![]() ,所以|BE|=|AE|,
,所以|BE|=|AE|,
所以直線AB的傾斜角為![]() ,所以直線AB的斜率為
,所以直線AB的斜率為![]() ,
,
所以直線![]() 的斜率為1,
的斜率為1,
因為點B的坐標(biāo)為![]() ,所以|BD|=
,所以|BD|=![]() .
.
(2)由題得A(21,0),設(shè)直線AB的斜率為![]() ,
,
所以直線AB的方程為![]() ,
,
因為|AC|=|BD|,
所以![]() .
.
由題得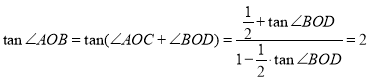 ,
,
所以![]() ,
,
所以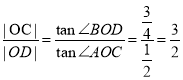 .
.
(3)由題得![]()
![]() ,
,
所以![]() ,
,
所以![]() .
.
因為![]() ,
,
所以![]()
解之得![]() .
.
故![]() 正切值的取值范圍為
正切值的取值范圍為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】隨著計算機的出現(xiàn),圖標(biāo)被賦予了新的含義,又有了新的用武之地.在計算機應(yīng)用領(lǐng)域,圖標(biāo)成了具有明確指代含義的計算機圖形.如圖所示的圖標(biāo)是一種被稱之為“黑白太陽”的圖標(biāo),該圖標(biāo)共分為3部分.第一部分為外部的八個全等的矩形,每一個矩形的長為3、寬為1;第二部分為圓環(huán)部分,大圓半徑為3,小圓半徑為2;第三部分為圓環(huán)內(nèi)部的白色區(qū)域.在整個“黑白太陽”圖標(biāo)中隨機取一點,則此點取自圖標(biāo)第三部分的概率為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,動圓
中,動圓![]() 與圓
與圓![]() 外切,且圓
外切,且圓![]() 與直線
與直線![]() 相切,記動圓圓心
相切,記動圓圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的軌跡方程;
的軌跡方程;
(2)設(shè)過定點![]() 的動直線
的動直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,試問:在曲線
兩點,試問:在曲線![]() 上是否存在點
上是否存在點![]() (與
(與![]() 兩點相異),當(dāng)直線
兩點相異),當(dāng)直線![]() 的斜率存在時,直線
的斜率存在時,直線![]() 的斜率之和為定值?若存在,求出點
的斜率之和為定值?若存在,求出點![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 的三邊分別為
的三邊分別為![]() 所對的角分別為
所對的角分別為![]() ,且三邊滿足
,且三邊滿足![]() ,已知
,已知![]() 的外接圓的面積為
的外接圓的面積為![]() ,設(shè)
,設(shè)![]() .則
.則![]() 的取值范圍為______,函數(shù)
的取值范圍為______,函數(shù)![]() 的最大值的取值范圍為_______.
的最大值的取值范圍為_______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 的內(nèi)角
的內(nèi)角![]() 、
、![]() 、
、![]() 的對邊分別為
的對邊分別為![]() 、
、![]() 、
、![]() ,
,![]() 為
為![]() 內(nèi)一點,若分別滿足下列四個條件:
內(nèi)一點,若分別滿足下列四個條件:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
則點![]() 分別為
分別為![]() 的( )
的( )
A.外心、內(nèi)心、垂心、重心B.內(nèi)心、外心、垂心、重心
C.垂心、內(nèi)心、重心、外心D.內(nèi)心、垂心、外心、重心
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
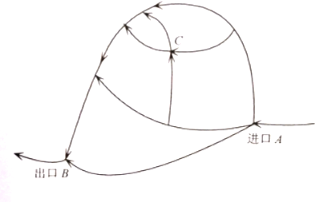
【題目】如圖是一旅游景區(qū)供游客行走的路線圖,假設(shè)從進口![]() 開始到出口
開始到出口![]() ,每遇到一個岔路口,每位游客選擇其中一條道路行進是等可能的.現(xiàn)有甲、乙、丙、丁共
,每遇到一個岔路口,每位游客選擇其中一條道路行進是等可能的.現(xiàn)有甲、乙、丙、丁共![]() 名游客結(jié)伴到旅游景區(qū)游玩,他們從進口
名游客結(jié)伴到旅游景區(qū)游玩,他們從進口![]() 的岔路口就開始選擇道路自行游玩,并按箭頭所指路線行走,最后到出口
的岔路口就開始選擇道路自行游玩,并按箭頭所指路線行走,最后到出口![]() 集中,設(shè)點
集中,設(shè)點![]() 是其中的一個交叉路口點.
是其中的一個交叉路口點.
(1)求甲經(jīng)過點![]() 的概率;
的概率;
(2)設(shè)這![]() 名游客中恰有
名游客中恰有![]() 名游客都是經(jīng)過點
名游客都是經(jīng)過點![]() ,求隨機變量
,求隨機變量![]() 的概率分布和數(shù)學(xué)期望.
的概率分布和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】古希臘雅典學(xué)派算學(xué)家歐道克薩斯提出了“黃金分割”的理論,利用尺規(guī)作圖可畫出己知線段的黃金分割點,具體方法如下:(l)取線段AB=2,過點B作AB的垂線,并用圓規(guī)在垂線上截取BC=![]() AB,連接AC;(2)以C為圓心,BC為半徑畫弧,交AC于點D;(3)以A為圓心,以AD為半徑畫弧,交AB于點E.則點E即為線段AB的黃金分割點.若在線段AB上隨機取一點F,則使得BE≤AF≤AE的概率約為( )(參考數(shù)據(jù):
AB,連接AC;(2)以C為圓心,BC為半徑畫弧,交AC于點D;(3)以A為圓心,以AD為半徑畫弧,交AB于點E.則點E即為線段AB的黃金分割點.若在線段AB上隨機取一點F,則使得BE≤AF≤AE的概率約為( )(參考數(shù)據(jù):![]() 2.236)
2.236)
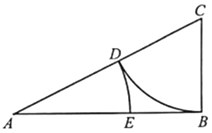
A. 0.236B. 0.382C. 0.472D. 0.618
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上,
上,![]() ,現(xiàn)將四邊形
,現(xiàn)將四邊形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(Ⅰ)若![]() ,在折疊后的線段
,在折疊后的線段![]() 上是否存在一點
上是否存在一點![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由;
的值;若不存在,說明理由;
(Ⅱ)當(dāng)三棱錐![]() 的體積最大時,求二面角
的體積最大時,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com