
【題目】如圖,已知橢圓C: ![]() ,點A,B分別是左、右頂點,過右焦點F的直線MN(異于x軸)交于橢圓C于M、N兩點.
,點A,B分別是左、右頂點,過右焦點F的直線MN(異于x軸)交于橢圓C于M、N兩點.
(1)若橢圓C過點 ,且右準線方程為
,且右準線方程為![]() ,求橢圓C的方程;
,求橢圓C的方程;
(2)若直線BN的斜率是直線AM斜率的2倍,求橢圓C的離心率.

【答案】(1) ![]() 或
或![]() ;(2)
;(2) ![]() .
.
【解析】試題分析:(1)根據曲線上的點和右準線方程寫出橢圓方程;(2)設![]() ,
, ![]() ,則
,則![]() ,
, ![]() ,
, ![]() ;因為點
;因為點![]() 在橢圓
在橢圓![]() 上,所以
上,所以![]() ,所以
,所以![]() ,聯立方程消元,根據韋達定理可得
,聯立方程消元,根據韋達定理可得 ,又
,又![]() ,進而求得離心率.
,進而求得離心率.
試題解析:(1)因為橢圓![]() 過點
過點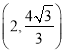 ,所以
,所以![]() ,
,
又已知右準線方程為![]() ,所以
,所以![]() ,
, ![]() ,
,
可解得![]() ,
, ![]() ;或
;或![]() ,
, ![]() ;
;
所以橢圓![]() 的方程為
的方程為![]() 或
或![]() .
.
(2)設![]() ,
, ![]() ,則
,則![]() ,
, ![]() ,
, ![]() ;
;
因為點![]() 在橢圓
在橢圓![]() 上,所以
上,所以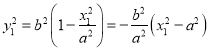 ,
,
所以![]() ,
,
設直線![]() :
: ![]() ,與橢圓
,與橢圓![]() :
: ![]() 聯立方程組消去
聯立方程組消去![]() 得
得
![]() ,
,
![]()
![]() ,
,
將![]() ,
, ![]() 代入上式化簡得
代入上式化簡得
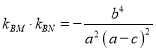 ,又
,又![]() ;所以
;所以 ,
,
得![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,即橢圓
,即橢圓![]() 的離心率為
的離心率為![]() .
.
點睛:本題考查直線與拋物線的位置關系的問題,其中過焦點的最短弦長為通徑. 直線與圓錐曲線的位置關系從幾何角度看:當直線與雙曲線的漸進線平行時,直線與雙曲線只有一個交點;當直線與拋物線的對稱軸平行或重合時,直線與拋物線也只有一個交點.從代數角度看:設直線L的方程與圓錐曲線的方程聯立得到![]() .若
.若![]() =0,當圓錐曲線是雙曲線時,直線L與雙曲線的漸進線平行或重合;當圓錐曲線是拋物線時,直線L與拋物線的對稱軸平行或重合.若
=0,當圓錐曲線是雙曲線時,直線L與雙曲線的漸進線平行或重合;當圓錐曲線是拋物線時,直線L與拋物線的對稱軸平行或重合.若![]() ,設
,設![]() .
. ![]() 時,直線和圓錐曲線相交于不同兩點,相交.
時,直線和圓錐曲線相交于不同兩點,相交. ![]() 時,直線和圓錐曲線相切于一點,相切.
時,直線和圓錐曲線相切于一點,相切. ![]() 時,直線和圓錐曲線沒有公共點,相離.
時,直線和圓錐曲線沒有公共點,相離.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐S﹣ABCD中,底面ABCD是菱形,∠BAD=60°,側面SAB⊥底面ABCD,并且SA=SB=AB=2,F為SD的中點. 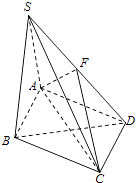
(1)求三棱錐S﹣FAC的體積;
(2)求直線BD與平面FAC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個袋子中裝有三個編號分別為1,2,3的紅球和三個編號分別為1,2,3的白球,三個紅球按其編號分別記為a1 , a2 , a3 , 三個白球按其編號分別記為b1 , b2 , b3 , 袋中的6個球除顏色和編號外沒有任何差異,現從袋中一次隨機地取出兩個球,
(1)列舉所有的基本事件,并寫出其個數;
(2)規定取出的紅球按其編號記分,取出的白球按其編號的2倍記分,取出的兩個球的記分之和為一次取球的得分,求一次取球的得分不小于6的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2 ![]() ﹣
﹣ ![]() ,則使得f(2x)>f(x﹣3)成立的x的取值范圍是( )
,則使得f(2x)>f(x﹣3)成立的x的取值范圍是( )
A.(﹣∞,﹣3)
B.(1,+∞)
C.(﹣3,﹣1)
D.(﹣∞,﹣3)∪(1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3﹣3x
(1)討論f(x)的單調區間;
(2)若函數g(x)=f(x)﹣m在[﹣ ![]() ,3]上有三個零點,求實數m的取值范圍;
,3]上有三個零點,求實數m的取值范圍;
(3)設函數h(x)=ex﹣ex+4n2﹣2n(e為自然對數的底數),如果對任意的x1 , x2∈[ ![]() ,2],都有f(x1)≤h(x2)恒成立,求實數n的取值范圍.
,2],都有f(x1)≤h(x2)恒成立,求實數n的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從1,3,5,7,9這五個數中,每次取出兩個不同的數分別記為a,b,共可得到lga﹣lgb的不同值的個數是( )
A.9
B.10
C.18
D.20
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x),當x,y∈R時,恒有f(x+y)=f(x)+f(y).當x>0時,f(x)>0
(1)求證:f(x)是奇函數;
(2)若 ![]() ,試求f(x)在區間[﹣2,6]上的最值;
,試求f(x)在區間[﹣2,6]上的最值;
(3)是否存在m,使f(2( ![]() )2﹣4)+f(4m﹣2(
)2﹣4)+f(4m﹣2( ![]() ))>0對任意x∈[1,2]恒成立?若存在,求出實數m的取值范圍;若不存在,說明理由.
))>0對任意x∈[1,2]恒成立?若存在,求出實數m的取值范圍;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com