
若數列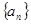 滿足
滿足 ,則當
,則當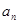 取最小值時
取最小值時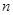 的值為( )
的值為( )
A. 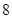 或
或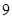 B.
B. 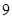 C.
C.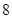 D.
D. 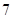 或
或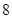
 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| sin2a3-cos2a3+cos2a3cos2a6-sin2a3sin2a6 |
| sin(a4+a5) |
| 4π |
| 3 |
| 3π |
| 2 |
| 4π |
| 3 |
| 3π |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2007年普通高等學校招生全國統一考試理科數學卷(上海) 題型:解答題
若有窮數列 (
( 是正整數),滿足
是正整數),滿足 即
即
( 是正整數,且
是正整數,且 ),就稱該數列為“對稱數列”。
),就稱該數列為“對稱數列”。
(1)已知數列 是項數為7的對稱數列,且
是項數為7的對稱數列,且 成等差數列,
成等差數列, ,試寫出
,試寫出 的每一項
的每一項
(2)已知 是項數為
是項數為 的對稱數列,且
的對稱數列,且 構成首項為50,公差為
構成首項為50,公差為 的等差數列,數列
的等差數列,數列 的前
的前 項和為
項和為 ,則當
,則當 為何值時,
為何值時, 取到最大值?最大值為多少?
取到最大值?最大值為多少?
(3)對于給定的正整數 ,試寫出所有項數不超過
,試寫出所有項數不超過 的對稱數列,使得
的對稱數列,使得 成為數列中的連續項;當
成為數列中的連續項;當 時,試求其中一個數列的前2008項和
時,試求其中一個數列的前2008項和
查看答案和解析>>
科目:高中數學 來源:2011-2012學年上海市崇明縣高三高考模擬考試二模理科數學試卷(解析版) 題型:解答題
已知數列 是各項均不為0的等差數列,公差為d,
是各項均不為0的等差數列,公差為d, 為其前n項和,且滿足
為其前n項和,且滿足 ,
, .數列
.數列 滿足
滿足 ,
, ,
, 為數列
為數列 的前n項和.
的前n項和.
(1)求數列 的通項公式
的通項公式 和數列
和數列 的前n項和
的前n項和 ;
;
(2)若對任意的 ,不等式
,不等式 恒成立,求實數
恒成立,求實數 的取值范圍;
的取值范圍;
(3)是否存在正整數
 ,使得
,使得 成等比數列?若存在,求出所有
成等比數列?若存在,求出所有 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【解析】第一問利用在 中,令n=1,n=2,
中,令n=1,n=2,
得 即
即
解得 ,,
,, [
[
又 時,
時, 滿足
滿足 ,
,
 ,
,

第二問,①當n為偶數時,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 ,等號在n=2時取得.
,等號在n=2時取得.
 此時
此時 需滿足
需滿足 .
.
②當n為奇數時,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 是隨n的增大而增大, n=1時
是隨n的增大而增大, n=1時 取得最小值-6.
取得最小值-6.
 此時
此時 需滿足
需滿足 .
.
第三問 ,
,
若 成等比數列,則
成等比數列,則 ,
,
即. 
由 ,可得
,可得 ,即
,即 ,
,
 .
. 
(1)(法一)在 中,令n=1,n=2,
中,令n=1,n=2,
得 即
即
解得 ,,
,, [
[
又 時,
時, 滿足
滿足 ,
,
 ,
,
 .
.
(2)①當n為偶數時,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 ,等號在n=2時取得.
,等號在n=2時取得.
 此時
此時 需滿足
需滿足 .
.
②當n為奇數時,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
 是隨n的增大而增大, n=1時
是隨n的增大而增大, n=1時 取得最小值-6.
取得最小值-6.
 此時
此時 需滿足
需滿足 .
.
綜合①、②可得 的取值范圍是
的取值范圍是 .
.
(3) ,
,
若 成等比數列,則
成等比數列,則 ,
,
即. 
由 ,可得
,可得 ,即
,即 ,
,
 .
. 
又 ,且m>1,所以m=2,此時n=12.
,且m>1,所以m=2,此時n=12.
因此,當且僅當m=2,
n=12時,數列 中的
中的 成等比數列
成等比數列
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com