
【題目】對于函數![]() 和
和![]() ,若存在區間
,若存在區間![]() ,使
,使![]() 在區間
在區間![]() 上恒成立,則稱區間
上恒成立,則稱區間![]() 是函數
是函數![]() 和
和![]() 的“公共鄰域”.設函數
的“公共鄰域”.設函數![]() 的反函數為
的反函數為![]() ,函數
,函數![]() 的圖像與函數
的圖像與函數![]() 的圖像關于點
的圖像關于點![]() 對稱.
對稱.
(1)求函數![]() 和
和![]() 的解析式;
的解析式;
(2)若![]() ,求函數
,求函數![]() 的定義域;
的定義域;
(3)是否存在實數![]() ,使得區間
,使得區間![]() 是
是![]() 和
和![]() 的“公共鄰域”,若存在,求出
的“公共鄰域”,若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)將![]() 作為方程利用指數式和對數式的互化解出
作為方程利用指數式和對數式的互化解出![]() ,然后確定原函數的值域即為反函數的定義域,再由對稱可得將
,然后確定原函數的值域即為反函數的定義域,再由對稱可得將![]() 換為
換為![]() ,
,![]() 換為
換為![]() ,即可得到所求
,即可得到所求![]() 的解析式;
的解析式;
(2)由對數的真數大于0,解不等式求交集,即可得到所求定義域;
(3)設![]() ,然后求出
,然后求出![]() 在閉區間
在閉區間![]() ,
,![]() 上的最小值與最大值,使最大值小于等于1,最小值大于等于
上的最小值與最大值,使最大值小于等于1,最小值大于等于![]() ,建立不等式組進行求解即可.
,建立不等式組進行求解即可.
解:(1)設![]() ,則
,則![]() ,
,
兩邊取對數得:![]() ,
,
所以![]() ;
;
由函數![]() 的圖象與函數
的圖象與函數![]() 的圖象 關于點
的圖象 關于點![]() 對稱,
對稱,
可得![]() ,即為
,即為![]() ;
;
(2)![]() ,函數
,函數![]() ,
,
由![]() ,且
,且![]() ,
,
可得![]() ,
,
則函數的定義域為![]() ;
;
(3)假設存在實數![]() ,使得區間
,使得區間![]() ,
,![]() 是
是![]() 和
和![]() 的“公共鄰域”,
的“公共鄰域”,
因為![]() ,
,![]() 時,函數有意義,
時,函數有意義,
所以![]() ,所以
,所以![]() ,
,
由區間![]() ,
,![]() 是
是![]() 和
和![]() 的“公共鄰域”,
的“公共鄰域”,
可得![]() ,
,
設![]() ,
,
二次函數![]() 的對稱軸為
的對稱軸為![]() ,
,
所以![]() 在
在![]() ,
,![]() 上為增函數,
上為增函數,
當![]() 時,取得最小值
時,取得最小值![]() ,當
,當![]() 時取得最大值
時取得最大值![]() ,
,
從而可得![]() 在閉區間
在閉區間![]() ,
,![]() 上的最小值與最大值分別為:
上的最小值與最大值分別為:
![]() ,
,![]() ,
,
當![]() ,
,![]() 時,恒有
時,恒有![]() 成立的充要條件為:
成立的充要條件為:
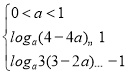 ,即為
,即為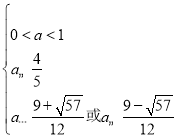 ,
,
解得![]() .
.
則存在實數![]() ,且
,且![]() ,
,
即![]() 時使得區間
時使得區間![]() ,
,![]() 是
是![]() 和
和![]() 的“公共鄰域”.
的“公共鄰域”.


科目:高中數學 來源: 題型:
【題目】已知函數![]() 的一系列對應值如下表:
的一系列對應值如下表:

(1)根據表格提供的數據求出函數![]() 的一個解析式;
的一個解析式;
(2)根據(1)的結果,若函數![]() 的周期為
的周期為![]() ,當
,當![]() 時,方程
時,方程![]() 恰有兩個不同的解,求實數
恰有兩個不同的解,求實數![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某群體的人均通勤時間,是指單日內該群體中成員從居住地到工作地的平均用時,某地上班族![]() 中的成員僅以自駕或公交方式通勤,分析顯示:當
中的成員僅以自駕或公交方式通勤,分析顯示:當![]() 中
中![]() 的成員自駕時,自駕群體的人均通勤時間為
的成員自駕時,自駕群體的人均通勤時間為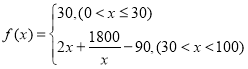 (單位:分鐘),而公交群體的人均通勤時間不受
(單位:分鐘),而公交群體的人均通勤時間不受![]() 影響,恒為40分鐘,試根據上述分析結果回答下列問題:
影響,恒為40分鐘,試根據上述分析結果回答下列問題:
(1)當![]() 在什么范圍內時,公交群體的人均通勤時間少于自駕群體的人均通勤時間?
在什么范圍內時,公交群體的人均通勤時間少于自駕群體的人均通勤時間?
(2)求該地上班族![]() 的人均通勤時間
的人均通勤時間![]() 的表達式;并求
的表達式;并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的邊AB所在直線方程為y=3x,BC所在直線方程為y=ax+12,AC邊上的高BD所在直線方程為y=﹣x+8.
(1)求實數a的值;
(2)若AC邊上的高BD![]() ,求邊AC所在的直線方程.
,求邊AC所在的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“活水圍網”養魚技術具有養殖密度高、經濟效益好的特點.研究表明:“活水圍網”養魚時,某種魚在一定的條件下,每尾魚的平均生長速度![]() (單位:千克/年)是養殖密度
(單位:千克/年)是養殖密度![]() (單位:尾/立方米)的函數.當
(單位:尾/立方米)的函數.當![]() 時,
時,![]() 的值為2千克/年;當
的值為2千克/年;當![]() 時,
時,![]() 是
是![]() 的一次函數;當
的一次函數;當![]() 時,因缺氧等原因,
時,因缺氧等原因,![]() 的值為0千克/年.
的值為0千克/年.
(1)當![]() 時,求
時,求![]() 關于
關于![]() 的函數表達式.
的函數表達式.
(2)當養殖密度![]() 為多少時,魚的年生長量(單位:千克/立方米)可以達到最大?并求出最大值.
為多少時,魚的年生長量(單位:千克/立方米)可以達到最大?并求出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《數書九章》中有“天池盆測雨”題,大概意思如下:在下雨時,用一個圓臺形的天池盆接雨水,天池盆盆口直徑為2尺8寸,盆底直徑為l尺2寸,盆深1尺8寸.若盆中積水深9寸,則平均降雨量是(注:①平均降雨量等于盆中積水體積除以盆口面積;②1尺等于10寸)( )
A. 3寸B. 4寸C. 5寸D. 6寸
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種計算機病毒是通過電子郵件進行傳播的,下表是某公司前5天監測到的數據:
第 | 1 | 2 | 3 | 4 | 5 |
被感染的計算機數量 | 10 | 20 | 39 | 81 | 160 |
則下列函數模型中,能較好地反映計算機在第![]() 天被感染的數量
天被感染的數量![]() 與
與![]() 之間的關系的是
之間的關系的是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學對高二甲、乙兩個同類班級進行“加強‘語文閱讀理解’訓練對提高‘數學應用題’得分率有幫助”的試驗,其中甲班為試驗班(加強語文閱讀理解訓練),乙班為對比班(常規教學,無額外訓練),在試驗前的測試中,甲、乙兩班學生在數學應用題上的得分率基本一致,試驗結束后,統計幾次數學應用題測試的平均成績(均取整數)如下表所示:
60分及以下 | 61~70分 | 71~80分 | 81~90分 | 91~100分 | |
甲班(人數) | 3 | 6 | 12 | 15 | 9 |
乙班(人數) | 4 | 7 | 16 | 12 | 6 |
現規定平均成績在80分以上(不含80分)的為優秀.
(1)由以上統計數據填寫![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為“加強‘語文閱讀理解’訓練對提高‘數學應用題’得分率”有幫助;
的把握認為“加強‘語文閱讀理解’訓練對提高‘數學應用題’得分率”有幫助;
(2)對甲乙兩班60分及以下的同學進行定期輔導,一個月后從中抽取3人課堂檢測,![]() 表示抽取到的甲班學生人數,求
表示抽取到的甲班學生人數,求![]() 及至少抽到甲班1名同學的概率.
及至少抽到甲班1名同學的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com